4 Introduction to R/Bioconductor
4.1 Installing packages
4.1.1 CRAN
The Comprehensive R Archive Network CRAN is the biggest archive of R packages. There are few requirements for uploading packages besides building and installing successfully, hence documentation and support is often minimal and figuring how to use these packages can be a challenge it itself. CRAN is the default repository R will search to find packages to install:
4.1.2 Github
Github isn’t specific to R, any code of any type in any state can be uploaded. There is no guarantee a package uploaded to github will even install, nevermind do what it claims to do. R packages can be downloaded and installed directly from github using the “devtools” package installed above.
Github is also a version control system which stores multiple versions of any package. By default the most recent “master” version of the package is installed. If you want an older version or the development branch this can be specified using the “ref” parameter:
Note: make sure you re-install the M3Drop master branch for later in the course.
4.1.3 Bioconductor
Bioconductor is a repository of R-packages specifically for biological analyses. It has the strictest requirements for submission, including installation on every platform and full documentation with a tutorial (called a vignette) explaining how the package should be used. Bioconductor also encourages utilization of standard data structures/classes and coding style/naming conventions, so that, in theory, packages and analyses can be combined into large pipelines or workflows.
Bioconductor also requires creators to support their packages and has a regular 6-month release schedule. Make sure you are using the most recent release of bioconductor before trying to install packages for the course.
4.1.4 Source
The final way to install packages is directly from source. In this case you have to download a fully built source code file, usually packagename.tar.gz, or clone the github repository and rebuild the package yourself. Generally this will only be done if you want to edit a package yourself, or if for some reason the former methods have failed.
4.2 Installation instructions
All the packages necessary for this course are available here. Starting from “RUN Rscript -e”install.packages(‘devtools’)” “, run each of the commands (minus”RUN”) on the command line or start an R session and run each of the commands within the quotation marks. Note the ordering of the installation is important in some cases, so make sure you run them in order from top to bottom.
4.3 Data types
As most of programming languages, R uses variables to store the data. The variable can be created by typing its name, assignment operator (= or <- that are mostly identical) and value:
## [1] 10we created variable named var that stores numerical value 10.
R variables might be of various types. There are more than 20 types in total, but normally only few of them are used directly: logical, integer, numeric, character, list, and S4. The former four represents atomic vectors that are simple data structures with values of one type. Lists and S4 variables allow to store more sophisticated data structures. Type of variable can be accessed using typeof function. Lets discuss atomic vectors first.
4.3.1 Logical
The logical type stores Boolean values, i.e. TRUE and FALSE. It is used for storing the results of logical operations and conditional statements will be coerced to this type.
## [1] "logical"## [1] TRUE## [1] FALSER has all usual logical operators
## [1] FALSE## [1] TRUE## [1] TRUE## [1] FALSE## [1] FALSE## [1] TRUE4.3.2 Numeric and integer
The numeric type is used to store decimal numbers.
## [1] "double"## [1] "double"## [1] "double"Here we see that even though R has an “integer” class and 42 could be stored more efficiently as an integer with notation used above it is stored as “numeric.” If we want 42 to be stored as an integer we must specify it using specific notation:
## [1] "integer"R have all common math operators and functions build in:
## [1] 5## [1] 12## [1] 2## [1] 25## [1] -0.9589243## [1] 2.2360684.3.3 Character
The character type stores text. Text variables can be created using single or double quotation marks, that are completely interchangeable:
## [1] "some text"## [1] "character"## [1] "another text. \"Double quotes\" can be used here"In addition to standard alphanumeric characters, strings can also store various special characters. Special characters are specified using a backlash followed by a single character, the most relevant are the special character for tab : \t and new line : \n:
## 'Hello World
## '## 'Hello World
## '## 'Hello
## World
## 'There are many text useful functions, let’s briefly discuss few of them:
## [1] "hello world"## [1] "hello_world"## [1] "hello"## [1] "goodbye world"## [1] TRUE## [1] FALSE4.3.4 These all are vectors!
Until now we stored just one value in each variable. But actually all types we just discussed are vectors, that is, they can store any number of values of given type. Function c can be used to create new vectors:
## [1] 1 3 -2## [1] "double"## [1] 4 5 6 7## [1] 10 9 8 7 6 5 4 3 2## [1] "hello" "world"## [1] "character"## [1] 2## [1] NA## [1] "hello" "world" "and" "goodbye"Vectors can store only values of the same type. In any attempt to combine values of different types they are auto-coerced to the rightmost type in the following sequence: logical -> integer -> numeric -> character:
## [1] TRUE FALSE## [1] "logical"## [1] 1 0 2## [1] "integer"## [1] 1.0 0.0 2.0 10.2## [1] "double"## [1] "TRUE" "FALSE" "2" "10.2" "text"## [1] "character"## [1] 2## [1] 1## [1] "double"## [1] FALSE FALSE FALSE FALSE FALSE TRUE TRUE TRUE TRUE TRUE## [1] 5## [1] 52.66183 55.15684 53.09312 64.80583 65.09491 46.97961 57.41312 67.22936
## [9] 70.98528 61.88919## [1] 5Exercise 1
What types will you get with following expressions (guess and check)
Answer
## [1] FALSE## [1] 2## [1] "45"## [1] 2.34.3.5 Vectorized operations
Since all basic types in R are vectors, operators and many functions are vectorized, that is, they perform operations for each element of vector arguments:
## [1] 1 4 9 16 25 36 49 64 81 100## [1] 5 8 9 8 5 0 -7 -16 -27 -40What would happen if lengths of operands are not identical?
## [1] 2 4 6 8 10 12 14 16 18 20## [1] 1 4 3 8 5 12 7 16 9 20## Warning in a * (1:3): longer object length is not a multiple of shorter object
## length## [1] 1 4 9 4 10 18 7 16 27 104.4 Named vectors
R allows elements of vectors to be named:
## a b other.name
## 1 3 10Names can be accessed and modified by names function:
## [1] "a" "b" "other.name"## newname b other.name
## 1 3 10## A B C
## 1 3 104.5 Vector subsetting
Vector subsetting is one of main advantages of R. It is very flexible and powerful. There are three types of subsetting: 1. By index (numerical) 2. By name (character) 3. By condition (logical) To make subsetting one need to type name of variable and specify desired elements in square brackets. ### Numerical subsetting Contrary to many other languages vector indexing in R is 1-based, that is, first element has index 1.
## [1] 9## [1] 1 9 10## [1] 24 1 10 1 4 24 24## [1] 4 7 9 10## [1] 100 24 10 9 7 4 1## [1] 10 10 1 4 7Negative indexes can be used to exclude specific elements:
## [1] 9 10 24 100## [1] 1 4 7 9 10 244.5.1 Subsetting by names
Named vectors can be indexed by names:
## a b c d e f g
## 1 4 7 9 10 24 100## a
## 1## b a c
## 4 1 7IMPORTANT! R allows name duplication. In this case first match will be returned:
## a b a d e f g
## 1 4 7 9 10 24 100## a
## 14.5.2 Logical subsetting
Logical subsetting used to conditionally select some elements. One can get all odd values for instance
## a a d
## 1 7 9## e f g
## 10 24 100Logical value in brackets should not necessary be calculated based on the vector
## a d f g
## 1 9 24 100## a a e g
## 1 7 10 100Exercise 2
- Get each third element from vector x
- Get only these values of vector x that are dividable by 4
- Get all elements of x which names are equal to ‘a’
Answer
## a f
## 7 24## a f
## 7 24## b f g
## 4 24 100## a a
## 1 74.6 Lists
Vectors can be used to store values of the same type. They would not work If one needs to store information of different types, name and age of a person for instance. R lists allows to store variable of any types, including other lists. Lists are very flexible (too flexible to be honest) and can fulfill all you needs. Lists can be created by list function that is analogous to c function.
## [[1]]
## [1] 1
##
## [[2]]
## [1] "a"
##
## [[3]]
## [1] 2 3 4
##
## [[4]]
## [1] "b" "c"## [1] "list"## List of 4
## $ : num 1
## $ : chr "a"
## $ : int [1:3] 2 3 4
## $ : chr [1:2] "b" "c"## List of 3
## $ name : chr "Sam"
## $ yob : int 2001
## $ weight: num 70.5## $weight
## [1] 70.5
##
## $yob
## [1] 2001## $weight
## [1] 70.5
##
## $name
## [1] "Sam"## $yob
## [1] 2001List indexing by [ operator returns sublist of the original list. To get specific element of of list [[ operator should be used:
## [1] "list"## $weight
## [1] 70.5## [1] "double"## [1] 70.5Operator [[ looks ugly, so for named vector one can use operator $ that is completely identical to [[:
## [1] "Sam"## [1] "character"Any types of data can be stored in list
## List of 3
## $ abc : chr [1:4] "a" "b" "c" "d"
## $ innerlist:List of 2
## ..$ a: chr "a"
## ..$ b: int [1:10] 1 2 3 4 5 6 7 8 9 10
## $ sumfun :function (..., na.rm = FALSE)## [1] 1 2 3 4 5 6 7 8 9 10## [1] 5 4 3 2 1## [1] 554.7 Dictionaries
Unlike python, R have no dictionary (hashtable) objects. In most cases named vectors (or lists) can be used instead (but be careful with name duplication). Otherwise one can use environments as hash, but it is out of scope of this course.
4.8 Classes/S3
R supports at least three different systems for object oriented programming (OOP). Most of R users do not need to create their own classes. But it is worth to know these systems to deal with existing packages. We will briefly discuss two of them: S3 and S4.
Lets start with S3 system. In OOP paradigm each variable is treated according to its class. R allows to add attributes to any variable. The attributes can be accessed, set and modified using attributes or attr functions.
## $names
## [1] "a" "b" "z"So, names of vector value are one of vector attribute. Normally, all attributes are accessed by specific functions such as names. S3 system uses attribute called class that can be accessed using function class. We will use factor class to illustrate S3 system. Factor is a class developed to store categorical information such as gender (male/female) or species (dog/cat/human). Categorical information can be stored as a text (that is OK in most of cases), but sometime factors are useful.
## [1] "integer"## [1] "factor"## [1] m m f
## Levels: m f unk## [1] "integer"## [1] 1 1 2
## attr(,"levels")
## [1] "m" "f" "unk"Some R functions (called generic, print for instance) can dispatch the function call, that is call specific function in dependence on its arguments. In this case it simply calls a functions with name that is combination of generic function name and class name separated by dot:
## [1] 1 1 2
## Levels: m f unkwhile f2 is not a factor now, it still can be printed as factor if we call corresponding function manually.
4.9 2d data structures
The types we discussed so far are one-dimensional, but some data (gene-to-cell expression matrix, or sample metadata) require 2d (or even Nd) structures (aka tables) to be stored. There are two 2d structures in R: arrays and data.frames. Arrays allows to store only values of a single type because internally arrays are vector. Data.frames can have columns of different types, while each column can contain values of only single type. Internally data.frames are lists of columns.
4.9.1 Arrays
## [,1] [,2] [,3]
## [1,] 1 5 9
## [2,] 2 6 10
## [3,] 3 7 11
## [4,] 4 8 12## [1] "integer"## [1] "matrix" "array"## $dim
## [1] 4 3## [1] 4 3## [1] 4## [1] 3## a b c
## A 1 5 9
## B 2 6 10
## C 3 7 11
## D 4 8 12Array subsetting can be performed using same three approaches (by numbers, by names and logically), but now indexes will apply to rows and columns separately:
## c b a
## A 9 5 1
## B 10 6 2## b c
## A 5 9
## B 6 10
## C 7 11
## D 8 12## a b c
## D 4 8 12
## B 2 6 10
## C 3 7 11## b b
## D 8 8
## C 7 7## a c
## A 1 9
## B 2 10
## C 3 11
## D 4 12## a b c
## C 3 7 11
## D 4 8 12## c b
## A 9 5
## C 11 7
## D 12 84.9.2 Data.frames
Data.frame is very similar to matrix but it allows to store values of different types in different columns. Data.frame can be created by data.frame function by specifying columns, all columns should be vectors of the same length.
## [1] "data.frame"## [1] "list"## name age sex
## 1 Sam 40 f
## 2 John 14 f
## 3 Sara 51 fSimilarly to arrays data.frames can have rownames and colnames. The only difference is that data.frame rownames should be unique:
## [1] "name" "age" "sex"## name age sex
## Sm Sam 40 f
## Jn John 14 f
## Sr Sara 51 fIndexing of data.frames is identical to array indexing:
## sex name
## Sr f Sara
## Sm f SamBut since data.frames are lists, operator $ can be used as well to get single column:
## [1] 40 14 514.10 S4 objects
S3 system allows to make functions which behavior depends on class of its first argument, but it cannot take into account other arguments. Additionally, S3 doesn’t allow to customize data structures, variables used in S3 system are atomic vectors or lists. S4 system allows to solve these problems. The main difference of S4 system compared do S3 is that in S4 each class have formal definition that describes what data are stored in the objects of this class (compare to S3 where you can assign any class to any variable). The data is stored in slots that have names and specified types. One need to specify slots to create new class:
Now we can create variable of this class
## [1] "Person"
## attr(,"package")
## [1] ".GlobalEnv"## [1] "S4"## An object of class "Person"
## Slot "name":
## [1] "John Smith"
##
## Slot "age":
## [1] 30Normally, slots can be accessed and modified by specific functions. For the class Person we specified above, one can expect function name to access name. But R allows to access slots directly using operator @ (that is not a good style but might be very convenient):
## [1] "John Smith"## [1] "name" "age"## [1] 30## [1] 30You can find more information about S4 classes (including how to create generic functions) here.
Exercise 3
1. What are type and classes of mtcars variable?
2. What attributes is has?
3. What attribute is used to store rownames? What is about colnames?
4. What are right functions to access these attributes?
5. Select all cars that have 4 cylinders
6. Select sub-table from mtcars that include cars with at least two carburetors and columns that names are three character long (use function nchar)
7. Calculate matrix of correlations between columns of mtcars by cm = cor(mtcars)
8. Answer Q1-3 for cm
mtcars is a toy dataset loaded automatically when R session starts.
Answer
# 1
class(mtcars)
type(mtcars)
# 2
attributes(mtcars)
# 3
# rownames are stored as row.names attribute
# colnames are stored as names (because mtcars is list, and column names are just names of the list elements)
# 4
rownames(mtcars)
colnames(mtcars)
# 5
mtcars[mtcars$cyl==4,]
# 6
nchar(colnames(mtcars))
mtcars[mtcars$carb>=2,nchar(colnames(mtcars))==3]
# 7
cm = cor(mtcars)
# 8
class(cm)
type(cm)
attributes(cm)
# rownames and colnames of array are stored as dimnames attribute (compare to data.frame above)4.11 More information
You can get more information about any R commands relevant to these datatypes using by typing ?function in an interactive session.
4.12 Tidy Data
4.12.1 What is Tidy Data?
Tidy data is a concept largely defined by Hadley Wickham (Wickham 2014). Tidy data has the following three characteristics:
- Each variable has its own column.
- Each observation has its own row.
- Each value has its own cell.
Here is an example of some tidy data:
## Students Subject Years Score
## 1 Mark Maths 1 5
## 2 Jane Biology 2 6
## 3 Mohammed Physics 3 4
## 4 Tom Maths 2 7
## 5 Celia Computing 3 9Here is an example of some untidy data:
## Students Sport Category Counts
## 1 Matt Tennis Wins 0
## 2 Matt Tennis Losses 1
## 3 Ellie Rugby Wins 3
## 4 Ellie Rugby Losses 2
## 5 Tim Football Wins 1
## 6 Tim Football Losses 4
## 7 Louise Swimming Wins 2
## 8 Louise Swimming Losses 2
## 9 Kelly Running Wins 5
## 10 Kelly Running Losses 1Task 1: In what ways is the untidy data not tidy? How could we make the untidy data tidy?
Tidy data is generally easier to work with than untidy data, especially if you are working with packages such as ggplot. Fortunately, packages are available to make untidy data tidy. Today we will explore a few of the functions available in the tidyr package which can be used to make untidy data tidy. If you are interested in finding out more about tidying data, we recommend reading “R for Data Science,” by Garrett Grolemund and Hadley Wickham. An electronic copy is available here: http://r4ds.had.co.nz/
The untidy data above is untidy because two variables (Wins and Losses) are stored in one column (Category). This is a common way in which data can be untidy. To tidy this data, we need to make Wins and Losses into columns, and store the values in Counts in these columns. Fortunately, there is a function from the tidyverse packages to perform this operation. The function is called spread, and it takes two arguments, key and value. You should pass the name of the column which contains multiple variables to key, and pass the name of the column which contains values from multiple variables to value. For example:
library(tidyverse)## Warning in system("timedatectl", intern = TRUE): running command 'timedatectl'
## had status 1sports<-data.frame(Students=c("Matt", "Matt", "Ellie", "Ellie", "Tim", "Tim", "Louise", "Louise", "Kelly", "Kelly"), Sport=c("Tennis","Tennis", "Rugby", "Rugby","Football", "Football","Swimming","Swimming", "Running", "Running"), Category=c("Wins", "Losses", "Wins", "Losses", "Wins", "Losses", "Wins", "Losses", "Wins", "Losses"), Counts=c(0,1,3,2,1,4,2,2,5,1))
sports## Students Sport Category Counts
## 1 Matt Tennis Wins 0
## 2 Matt Tennis Losses 1
## 3 Ellie Rugby Wins 3
## 4 Ellie Rugby Losses 2
## 5 Tim Football Wins 1
## 6 Tim Football Losses 4
## 7 Louise Swimming Wins 2
## 8 Louise Swimming Losses 2
## 9 Kelly Running Wins 5
## 10 Kelly Running Losses 1spread(sports, key=Category, value=Counts)## Students Sport Losses Wins
## 1 Ellie Rugby 2 3
## 2 Kelly Running 1 5
## 3 Louise Swimming 2 2
## 4 Matt Tennis 1 0
## 5 Tim Football 4 1Task 2: The dataframe foods defined below is untidy. Work out why and use spread() to tidy it
foods<-data.frame(student=c("Antoinette","Antoinette","Taylor", "Taylor", "Alexa", "Alexa"), Category=c("Dinner", "Dessert", "Dinner", "Dessert", "Dinner","Dessert"), Frequency=c(3,1,4,5,2,1))The other common way in which data can be untidy is if the columns are values instead of variables. For example, the dataframe below shows the percentages some students got in tests they did in May and June. The data is untidy because the columns May and June are values, not variables.
percentages<-data.frame(student=c("Alejandro", "Pietro", "Jane"), "May"=c(90,12,45), "June"=c(80,30,100))Fortunately, there is a function in the tidyverse packages to deal with this problem too. gather() takes the names of the columns which are values, the key and the value as arguments. This time, the key is the name of the variable with values as column names, and the value is the name of the variable with values spread over multiple columns. Ie:
gather(percentages, "May", "June", key="Month", value = "Percentage")## student Month Percentage
## 1 Alejandro May 90
## 2 Pietro May 12
## 3 Jane May 45
## 4 Alejandro June 80
## 5 Pietro June 30
## 6 Jane June 100These examples don’t have much to do with single-cell RNA-seq analysis, but are designed to help illustrate the features of tidy and untidy data. You will find it much easier to analyse your single-cell RNA-seq data if your data is stored in a tidy format. Fortunately, the data structures we commonly use to facilitate single-cell RNA-seq analysis usually encourage store your data in a tidy manner.
4.12.2 What is Rich Data?
If you google ‘rich data,’ you will find lots of different definitions for this term. In this course, we will use ‘rich data’ to mean data which is generated by combining information from multiple sources. For example, you could make rich data by creating an object in R which contains a matrix of gene expression values across the cells in your single-cell RNA-seq experiment, but also information about how the experiment was performed. Objects of the SingleCellExperiment class, which we will discuss below, are an example of rich data.
4.12.3 SingleCellExperiment class
SingleCellExperiment (SCE) is a S4 class for storing data from single-cell experiments. This includes specialized methods to store and retrieve spike-in information, dimensionality reduction coordinates and size factors for each cell, along with the usual metadata for genes and libraries.
In practice, an object of this class can be created using its constructor:
library(SingleCellExperiment)
counts <- matrix(rpois(100, lambda = 10), ncol=10, nrow=10)
rownames(counts) <- paste("gene", 1:10, sep = "")
colnames(counts) <- paste("cell", 1:10, sep = "")
sce <- SingleCellExperiment(
assays = list(counts = counts),
rowData = data.frame(gene_names = paste("gene_name", 1:10, sep = "")),
colData = data.frame(cell_names = paste("cell_name", 1:10, sep = ""))
)
sce## class: SingleCellExperiment
## dim: 10 10
## metadata(0):
## assays(1): counts
## rownames(10): gene1 gene2 ... gene9 gene10
## rowData names(1): gene_names
## colnames(10): cell1 cell2 ... cell9 cell10
## colData names(1): cell_names
## reducedDimNames(0):
## mainExpName: NULL
## altExpNames(0):In the SingleCellExperiment, users can assign arbitrary names to entries of assays. To assist interoperability between packages, some suggestions for what the names should be for particular types of data are provided by the authors:
- counts: Raw count data, e.g., number of reads or transcripts for a particular gene.
- normcounts: Normalized values on the same scale as the original counts. For example, counts divided by cell-specific size factors that are centred at unity.
- logcounts: Log-transformed counts or count-like values. In most cases, this will be defined as log-transformed normcounts, e.g., using log base 2 and a pseudo-count of 1.
- cpm: Counts-per-million. This is the read count for each gene in each cell, divided by the library size of each cell in millions.
- tpm: Transcripts-per-million. This is the number of transcripts for each gene in each cell, divided by the total number of transcripts in that cell (in millions).
Each of these suggested names has an appropriate getter/setter method for convenient manipulation of the SingleCellExperiment. For example, we can take the (very specifically named) counts slot, normalise it and assign it to normcounts instead:
normcounts(sce) <- log2(counts(sce) + 1)
sce## class: SingleCellExperiment
## dim: 10 10
## metadata(0):
## assays(2): counts normcounts
## rownames(10): gene1 gene2 ... gene9 gene10
## rowData names(1): gene_names
## colnames(10): cell1 cell2 ... cell9 cell10
## colData names(1): cell_names
## reducedDimNames(0):
## mainExpName: NULL
## altExpNames(0):dim(normcounts(sce))## [1] 10 10head(normcounts(sce))## cell1 cell2 cell3 cell4 cell5 cell6 cell7 cell8
## gene1 3.169925 3.169925 2.000000 2.584963 2.584963 3.321928 3.584963 3.321928
## gene2 3.459432 1.584963 3.584963 3.807355 3.700440 3.700440 3.000000 3.807355
## gene3 3.000000 3.169925 3.807355 3.169925 3.321928 3.321928 3.321928 2.584963
## gene4 3.584963 3.459432 3.000000 3.807355 3.700440 3.700440 3.700440 3.169925
## gene5 3.906891 3.000000 3.169925 3.321928 3.584963 3.459432 3.807355 3.807355
## gene6 3.700440 3.700440 3.584963 4.000000 3.169925 3.000000 3.459432 3.321928
## cell9 cell10
## gene1 3.807355 2.807355
## gene2 3.700440 4.000000
## gene3 4.000000 3.700440
## gene4 3.584963 3.700440
## gene5 2.584963 3.584963
## gene6 3.459432 4.0000004.12.4 scater package
scater is a R package for single-cell RNA-seq analysis (McCarthy et al. 2017). The package contains several useful methods for quality control, visualisation and pre-processing of data prior to further downstream analysis.
scater features the following functionality:
- Automated computation of QC metrics
- Transcript quantification from read data with pseudo-alignment
- Data format standardisation
- Rich visualizations for exploratory analysis
- Seamless integration into the Bioconductor universe
- Simple normalisation methods
We highly recommend to use scater for all single-cell RNA-seq analyses and scater is the basis of the first part of the course.
As illustrated in the figure below, scater will help you with quality control, filtering and normalization of your expression matrix following mapping and alignment. Keep in mind that this figure represents the original version of scater where an SCESet class was used. In the newest version this figure is still correct, except that SCESet can be substituted with the SingleCellExperiment class.
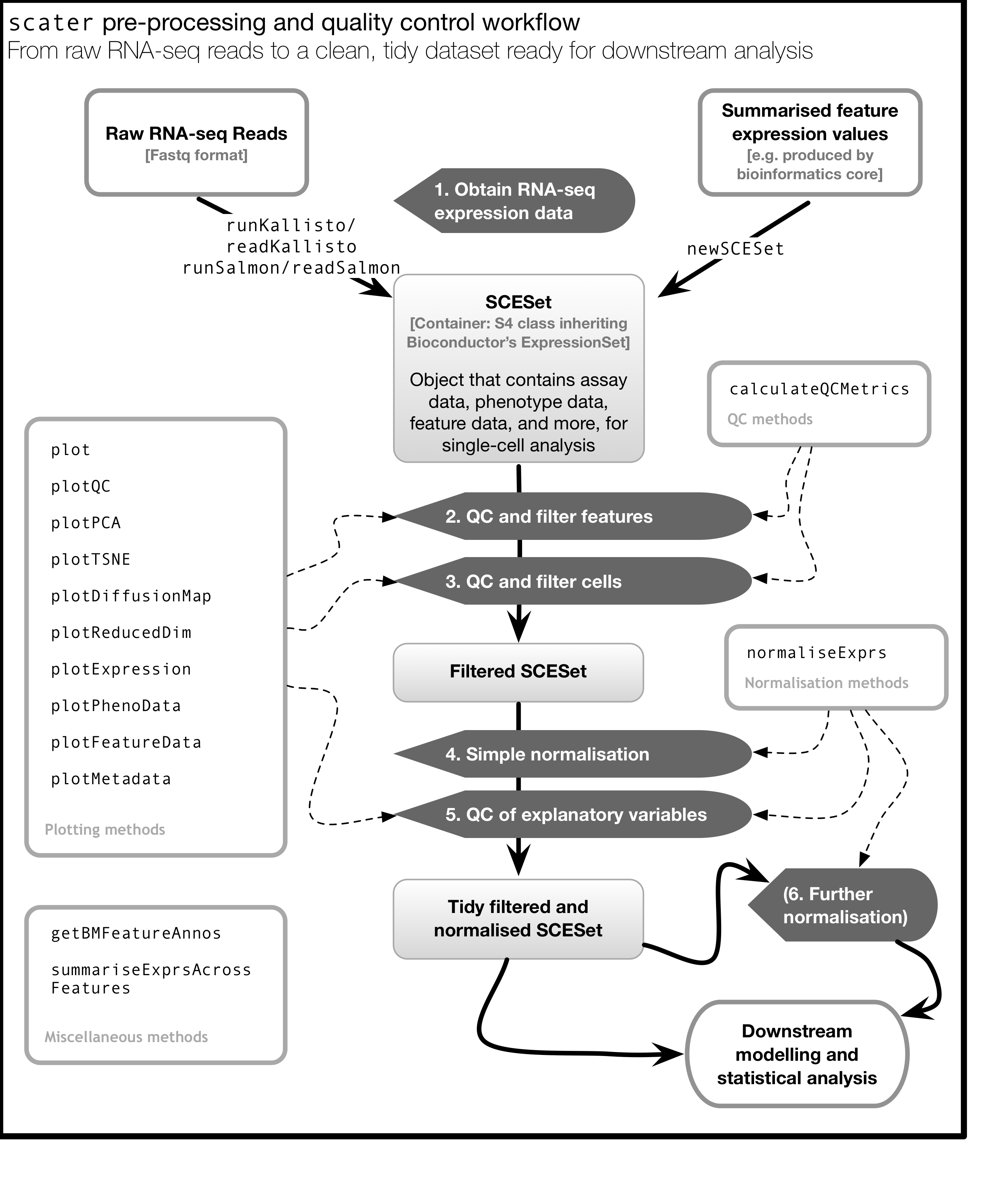
4.13 An Introduction to ggplot2
4.13.1 What is ggplot2?
ggplot2 is an R package designed by Hadley Wickham which facilitates data plotting. In this lab, we will touch briefly on some of the features of the package. If you would like to learn more about how to use ggplot2, we would recommend reading “ggplot2 Elegant graphics for data analysis,” by Hadley Wickham.
4.13.2 Principles of ggplot2
- Your data must be a dataframe if you want to plot it using ggplot2.
- Use the
aesmapping function to specify how variables in the dataframe map to features on your plot - Use geoms to specify how your data should be represented on your graph eg. as a scatterplot, a barplot, a boxplot etc.
4.13.3 Using the aes mapping function
The aes function specifies how variables in your dataframe map to features on your plot. To understand how this works, let’s look at an example:
library(ggplot2)
library(tidyverse)## Warning in system("timedatectl", intern = TRUE): running command 'timedatectl'
## had status 1set.seed(1)
counts <- as.data.frame(matrix(rpois(100, lambda = 10), ncol=10, nrow=10))
Gene_ids <- paste("gene", 1:10, sep = "")
colnames(counts) <- paste("cell", 1:10, sep = "")
counts<-data.frame(Gene_ids, counts)
counts## Gene_ids cell1 cell2 cell3 cell4 cell5 cell6 cell7 cell8 cell9 cell10
## 1 gene1 8 8 3 5 5 9 11 9 13 6
## 2 gene2 10 2 11 13 12 12 7 13 12 15
## 3 gene3 7 8 13 8 9 9 9 5 15 12
## 4 gene4 11 10 7 13 12 12 12 8 11 12
## 5 gene5 14 7 8 9 11 10 13 13 5 11
## 6 gene6 12 12 11 15 8 7 10 9 10 15
## 7 gene7 11 11 14 11 11 5 9 13 13 7
## 8 gene8 9 12 9 8 6 14 7 12 12 10
## 9 gene9 14 12 11 7 10 10 8 14 7 10
## 10 gene10 11 10 9 7 11 16 8 7 7 4ggplot(data = counts, mapping = aes(x = cell1, y = cell2))
Let’s take a closer look at the final command, ggplot(data = counts, mapping = aes(x = cell1, y = cell2)). ggplot() initialises a ggplot object and takes the arguments data and mapping. We pass our dataframe of counts to data and use the aes() function to specify that we would like to use the variable cell1 as our x variable and the variable cell2 as our y variable.
Task 1: Modify the command above to initialise a ggplot object where cell10 is the x variable and cell8 is the y variable.
Clearly, the plots we have just created are not very informative because no data is displayed on them. To display data, we will need to use geoms.
4.13.4 Geoms
We can use geoms to specify how we would like data to be displayed on our graphs. For example, our choice of geom could specify that we would like our data to be displayed as a scatterplot, a barplot or a boxplot.
Let’s see how our graph would look as a scatterplot.
ggplot(data = counts, mapping = aes(x = cell1, y = cell2)) + geom_point()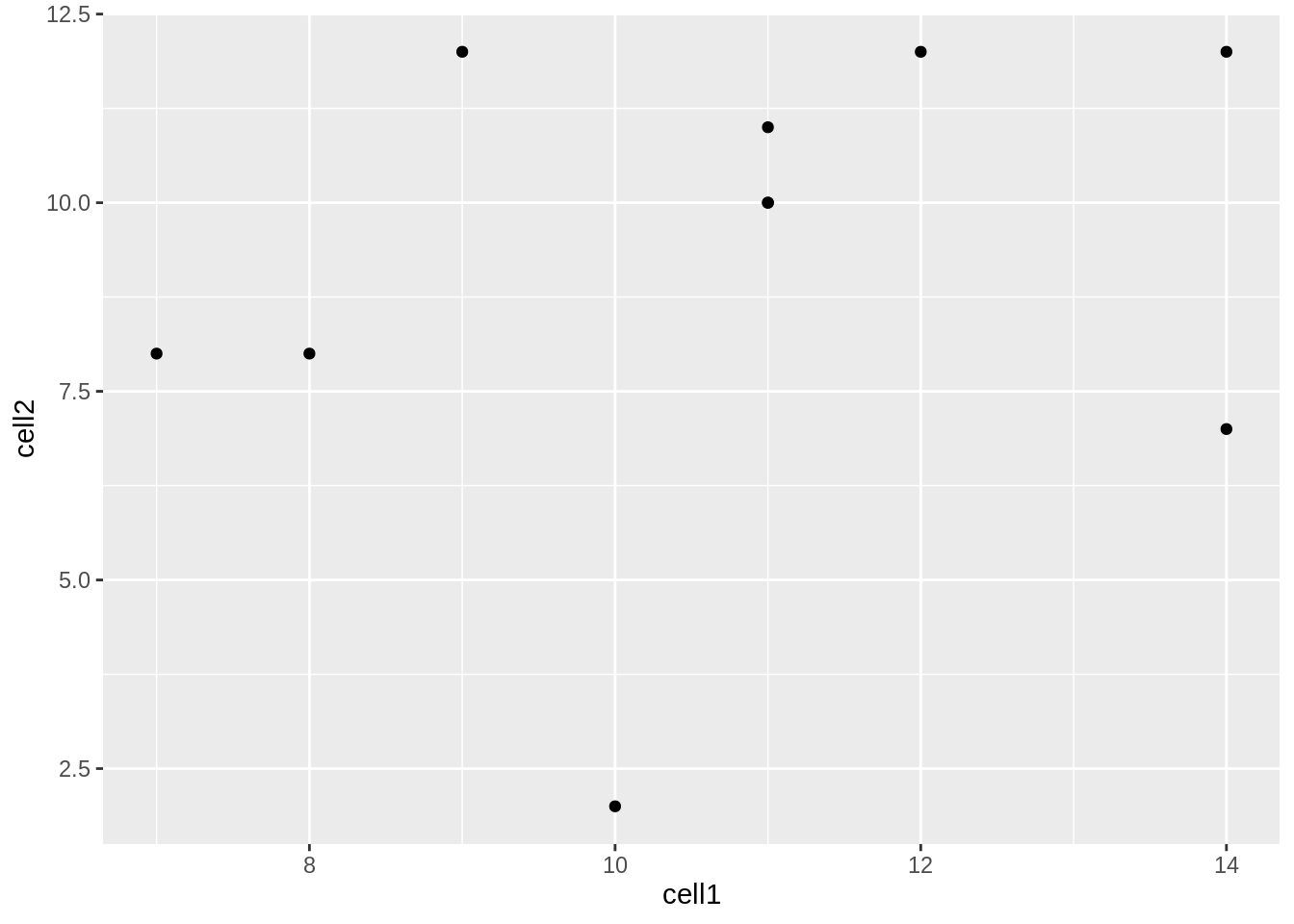
Now we can see that there doesn’t seem to be any correlation between gene expression in cell1 and cell2. Given we generated counts randomly, this isn’t too surprising.
Task 2: Modify the command above to create a line plot. Hint: execute ?ggplot and scroll down the help page. At the bottom is a link to the ggplot package index. Scroll through the index until you find the geom options.
4.13.5 Plotting data from more than 2 cells
So far we’ve been considering the gene counts from 2 of the cells in our dataframe. But there are actually 10 cells in our dataframe and it would be nice to compare all of them. What if we wanted to plot data from all 10 cells at the same time?
At the moment we can’t do this because we are treating each individual cell as a variable and assigning that variable to either the x or the y axis. We could create a 10 dimensional graph to plot data from all 10 cells on, but this is a) not possible to do with ggplot and b) not very easy to interpret. What we could do instead is to tidy our data so that we had one variable representing cell ID and another variable representing gene counts, and plot those against each other. In code, this would look like:
counts<-gather(counts, colnames(counts)[2:11], key = 'Cell_ID', value='Counts')
head(counts)## Gene_ids Cell_ID Counts
## 1 gene1 cell1 8
## 2 gene2 cell1 10
## 3 gene3 cell1 7
## 4 gene4 cell1 11
## 5 gene5 cell1 14
## 6 gene6 cell1 12Essentially, the problem before was that our data was not tidy because one variable (Cell_ID) was spread over multiple columns. Now that we’ve fixed this problem, it is much easier for us to plot data from all 10 cells on one graph.
ggplot(counts,aes(x=Cell_ID, y=Counts)) + geom_boxplot()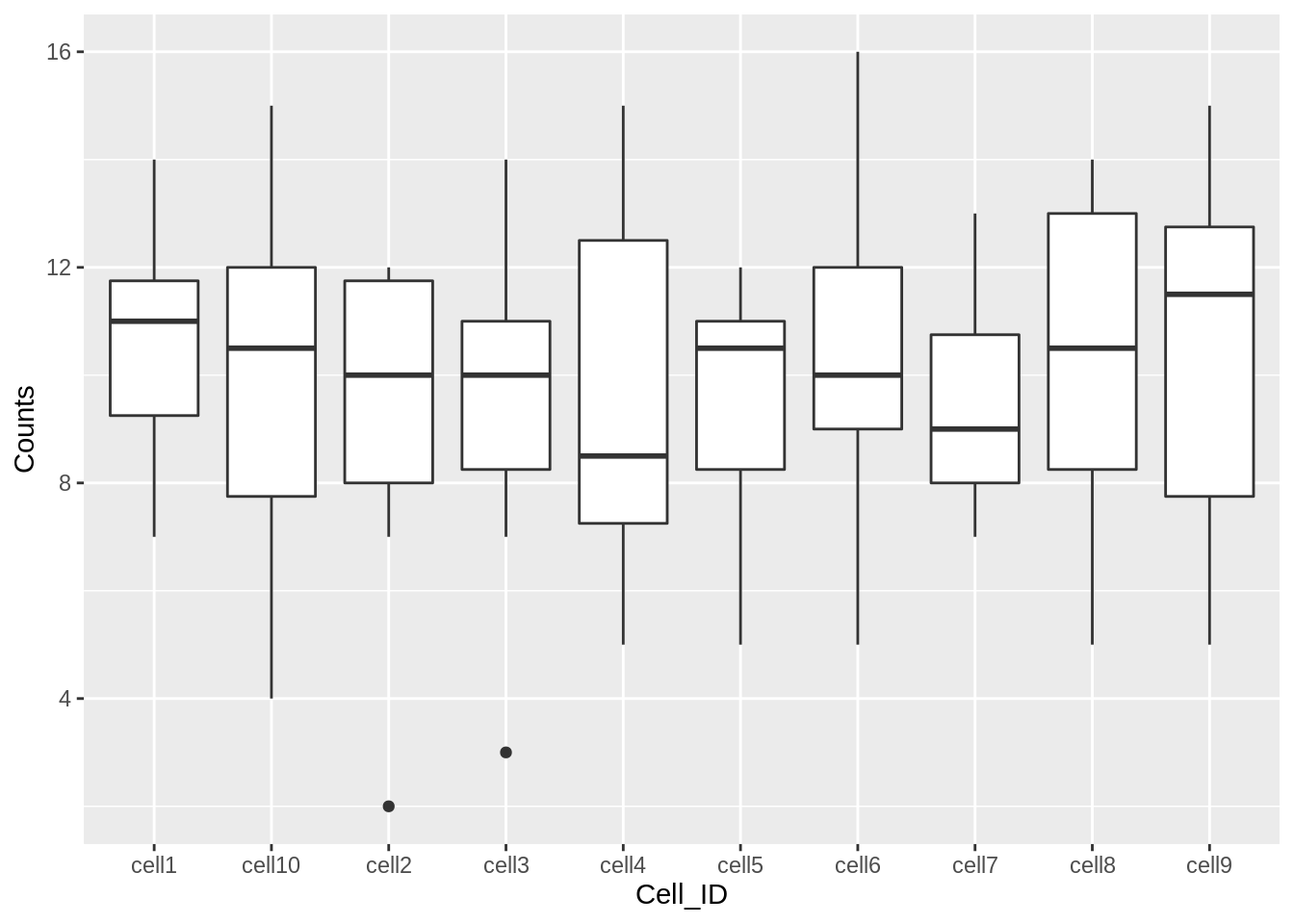
Task 3: Use the updated counts dataframe to plot a barplot with Cell_ID as the x variable and Counts as the y variable. Hint: you may find it helpful to read ?geom_bar.
Task 4: Use the updated counts dataframe to plot a scatterplot with Gene_ids as the x variable and Counts as the y variable.
4.13.6 Plotting heatmaps
A common method for visualising gene expression data is with a heatmap. Here we will use the R package pheatmap to perform this analysis with some gene expression data we will name test.
library(pheatmap)
set.seed(2)
test = matrix(rnorm(200), 20, 10)
test[1:10, seq(1, 10, 2)] = test[1:10, seq(1, 10, 2)] + 3
test[11:20, seq(2, 10, 2)] = test[11:20, seq(2, 10, 2)] + 2
test[15:20, seq(2, 10, 2)] = test[15:20, seq(2, 10, 2)] + 4
colnames(test) = paste("Cell", 1:10, sep = "")
rownames(test) = paste("Gene", 1:20, sep = "")
pheatmap(test)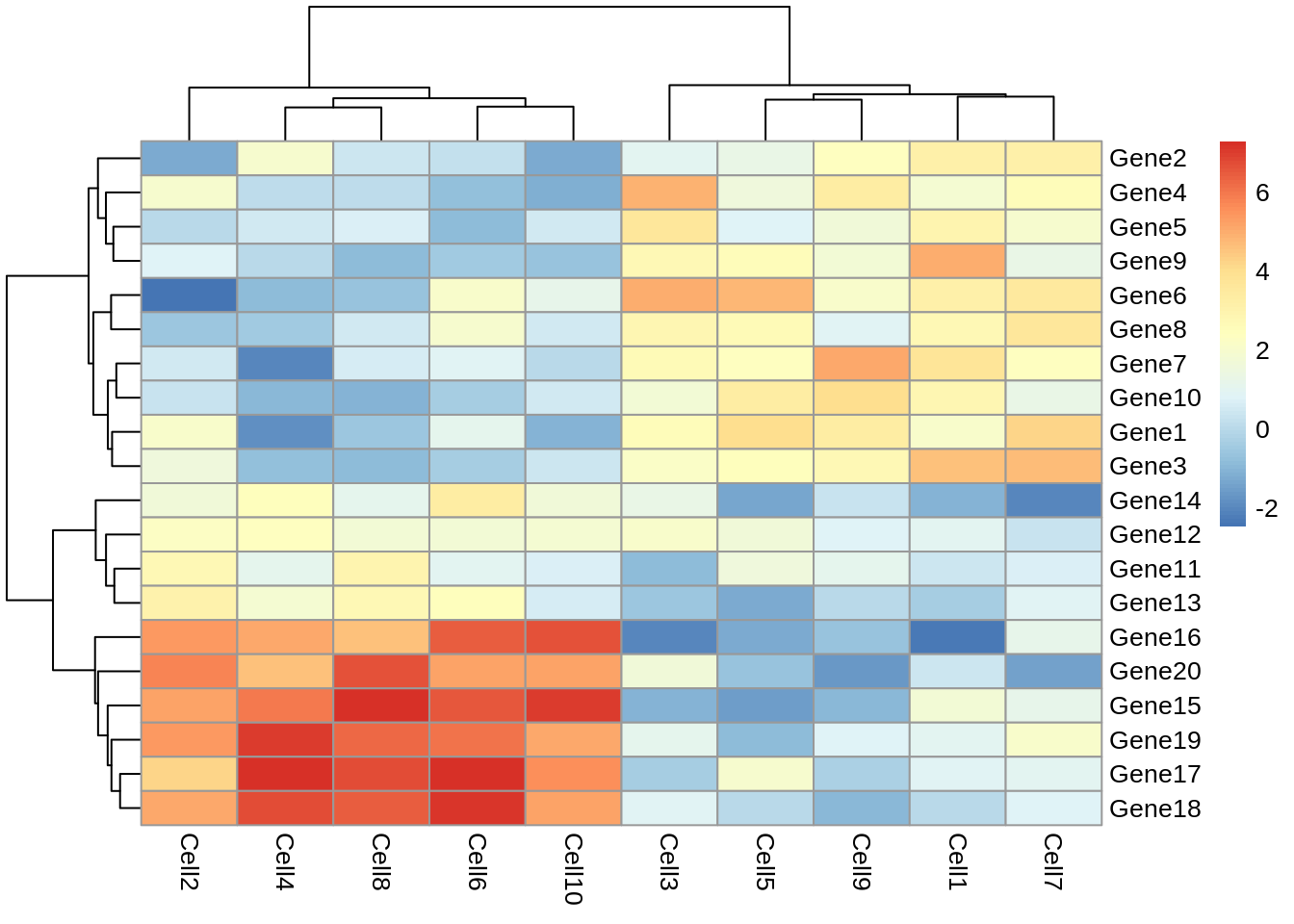
Let’s take a moment to work out what this graphic is showing us. Each row represents a gene and each column represents a cell. How highly expressed each gene is in each cell is represented by the colour of the corresponding box. For example, we can tell from this plot that gene18 is highly expressed in cell10 but lowly expressed in cell1.
This plot also gives us information on the results of a clustering algorithm. In general, clustering algorithms aim to split datapoints (eg.cells) into groups whose members are more alike one another than they are alike the rest of the datapoints. The trees drawn on the top and left hand sides of the graph are the results of clustering algorithms and enable us to see, for example, that cells 4,8,2,6 and 10 are more alike one another than they are alike cells 7,3,5,1 and 9. The tree on the left hand side of the graph represents the results of a clustering algorithm applied to the genes in our dataset.
If we look closely at the trees, we can see that eventually they have the same number of branches as there are cells and genes. In other words, the total number of cell clusters is the same as the total number of cells, and the total number of gene clusters is the same as the total number of genes. Clearly, this is not very informative, and will become impractical when we are looking at more than 10 cells and 20 genes. Fortunately, we can set the number of clusters we see on the plot. Let’s try setting the number of gene clusters to 2:
pheatmap(test, kmeans_k = 2)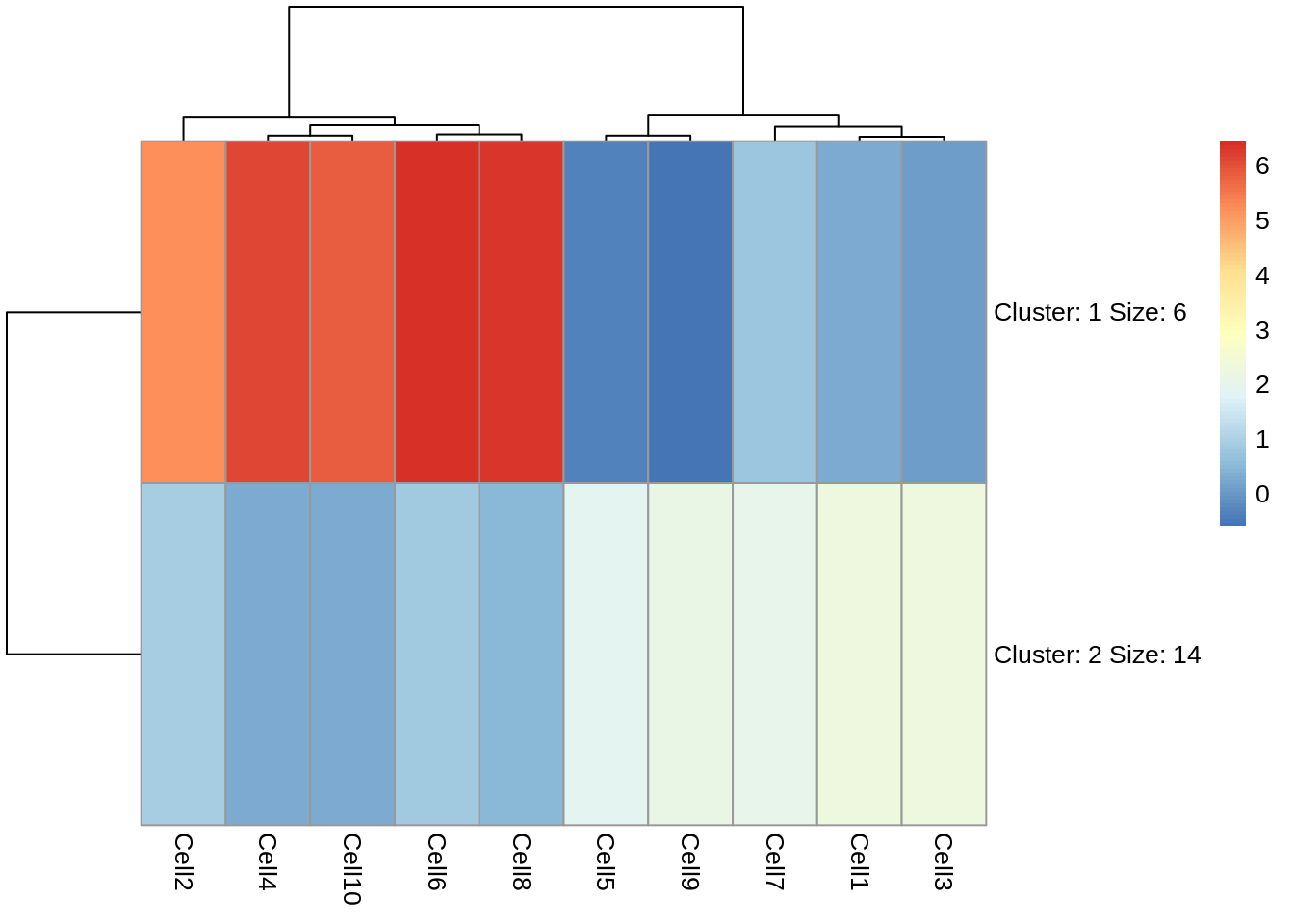
Now we can see that the genes fall into two clusters - a cluster of 8 genes which are upregulated in cells 2, 10, 6, 4 and 8 relative to the other cells and a cluster of 12 genes which are downregulated in cells 2, 10, 6, 4 and 8 relative to the other cells.
Task 5: Try setting the number of clusters to 3. Which number of clusters do you think is more informative?
4.13.7 Principal Component Analysis
Principal component analysis (PCA) is a statistical procedure that uses a transformation to convert a set of observations into a set of values of linearly uncorrelated variables called principal components. The transformation is carried out so that the first principle component accounts for as much of the variability in the data as possible, and each following principle component accounts for the greatest amount of variance possible under the contraint that it must be orthogonal to the previous components.
PCA plots are a good way to get an overview of your data, and can sometimes help identify confounders which explain a high amount of the variability in your data. We will investigate how we can use PCA plots in single-cell RNA-seq analysis in more depth in a future lab, here the aim is to give you an overview of what PCA plots are and how they are generated.
Let’s make a PCA plot for our test data. We can use the ggfortify package to let ggplot know how to interpret principle components.
library(ggfortify)
Principal_Components<-prcomp(test)
autoplot(Principal_Components, label=TRUE)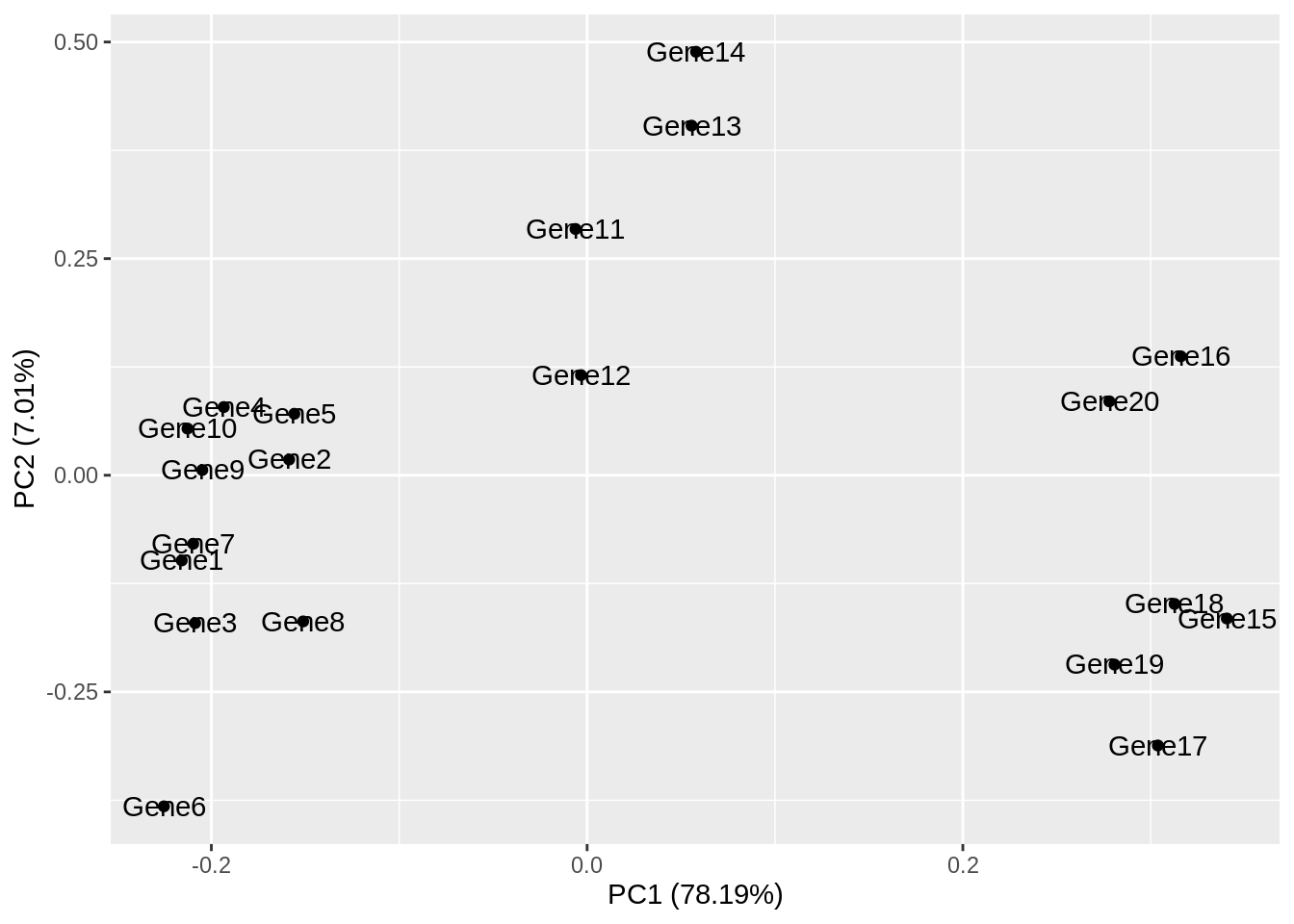
Task 6: Compare your clusters to the pheatmap clusters. Are they related? (Hint: have a look at the gene tree for the first pheatmap we plotted)
Task 7: Produce a heatmap and PCA plot for counts (below):
set.seed(1)
counts <- as.data.frame(matrix(rpois(100, lambda = 10), ncol=10, nrow=10))
rownames(counts) <- paste("gene", 1:10, sep = "")
colnames(counts) <- paste("cell", 1:10, sep = "")