6 Basic Quality Control (QC) and Exploration of scRNA-seq Datasets
6.1 Dataset Contruction and QC
6.1.1 Introduction
Once gene expression has been quantified it is summarized as an expression matrix where each row corresponds to a gene (or transcript) and each column corresponds to a single cell. In the next step, the matrix should be examined to remove poor quality cells. Failure to remove low quality cells at this stage may add technical noise which has the potential to obscure the biological signals of interest in the downstream analysis.
Since there is currently no standard method for performing scRNA-seq, the expected values for the various QC measures that will be presented here can vary substantially from experiment to experiment. Thus, to perform QC we will be looking for cells which are outliers with respect to the rest of the dataset rather than comparing to independent quality standards. Consequently, care should be taken when comparing quality metrics across datasets sequenced using different protocols.
6.1.2 Tung Dataset
To illustrate cell QC, we consider a dataset of induced pluripotent stem cells generated from three different individuals (Tung et al. 2017) in Yoav Gilad’s lab at the University of Chicago. The experiments were carried out on the Fluidigm C1 platform and to facilitate the quantification both unique molecular identifiers (UMIs) and ERCC spike-ins were used. Due to rapid increase in droplet-based method use, spike-ins are not widely used anymore; however, they can serve as an informative control for low throughput methods. The data files are located in the tung folder in your working directory. These files are the copies of the original files made on the 15/03/16. We will use these copies for reproducibility purposes.
We’ll use scater package, as well as AnnotationDbi and org.Hs.eg.db to convert ENSEMBL IDs into gene names (symbols).
library(scater)
library(SingleCellExperiment)
library(AnnotationDbi)
library(org.Hs.eg.db)
library(EnsDb.Hsapiens.v86)Next we’ll read in the matrix and the per-cell annotation. The latter is converted to factors on the fly.
molecules <- read.delim("data/tung/molecules.txt",row.names=1)
annotation <- read.delim("data/tung/annotation.txt",stringsAsFactors = T)Take a quick look at the dataset:
head(molecules[,1:3])## NA19098.r1.A01 NA19098.r1.A02 NA19098.r1.A03
## ENSG00000237683 0 0 0
## ENSG00000187634 0 0 0
## ENSG00000188976 3 6 1
## ENSG00000187961 0 0 0
## ENSG00000187583 0 0 0
## ENSG00000187642 0 0 0head(annotation)## individual replicate well batch sample_id
## 1 NA19098 r1 A01 NA19098.r1 NA19098.r1.A01
## 2 NA19098 r1 A02 NA19098.r1 NA19098.r1.A02
## 3 NA19098 r1 A03 NA19098.r1 NA19098.r1.A03
## 4 NA19098 r1 A04 NA19098.r1 NA19098.r1.A04
## 5 NA19098 r1 A05 NA19098.r1 NA19098.r1.A05
## 6 NA19098 r1 A06 NA19098.r1 NA19098.r1.A06Here we set altExp to contain ERCC, removing ERCC features from the main object:
umi <- SingleCellExperiment(assays = list(counts = as.matrix(molecules)), colData = annotation)
altExp(umi,"ERCC") <- umi[grep("^ERCC-",rownames(umi)), ]
umi <- umi[grep("^ERCC-",rownames(umi),invert = T), ]Now, let’s map ENSEMBL IDs to gene symbols. From the table command, we can see that most genes were annotated; however, 846 returned “NA.” By default, mapIds returs one symbol per ID; this behaviour can be changed using multiVals argument.
gene_names <- mapIds(org.Hs.eg.db, keys=rownames(umi), keytype="ENSEMBL", columns="SYMBOL",column="SYMBOL")## 'select()' returned 1:many mapping between keys and columnsrowData(umi)$SYMBOL <- gene_names
table(is.na(gene_names))##
## FALSE TRUE
## 18078 860Let’s remove all genes for which no symbols were found:
umi <- umi[! is.na(rowData(umi)$SYMBOL),]Let’s check if we can find mitochondrial proteins in the newly annotated symbols.
grep("^MT-",rowData(umi)$SYMBOL,value = T)## named character(0)Strangely, this returns nothing. Similar command to find ribosomal proteins (which start with RPL or RPS) works as expected:
grep("^RP[LS]",rowData(umi)$SYMBOL,value = T)## ENSG00000116251 ENSG00000142676 ENSG00000117676 ENSG00000142937 ENSG00000122406
## "RPL22" "RPL11" "RPS6KA1" "RPS8" "RPL5"
## ENSG00000177954 ENSG00000136643 ENSG00000138326 ENSG00000177600 ENSG00000166441
## "RPS27" "RPS6KC1" "RPS24" "RPLP2" "RPL27A"
## ENSG00000110700 ENSG00000162302 ENSG00000175634 ENSG00000149273 ENSG00000118181
## "RPS13" "RPS6KA4" "RPS6KB2" "RPS3" "RPS25"
## ENSG00000197728 ENSG00000229117 ENSG00000089009 ENSG00000089157 ENSG00000122026
## "RPS26" "RPL41" "RPL6" "RPLP0" "RPL21"
## ENSG00000165496 ENSG00000213741 ENSG00000165502 ENSG00000198208 ENSG00000100784
## "RPL10L" "RPS29" "RPL36AL" "RPS6KL1" "RPS6KA5"
## ENSG00000185088 ENSG00000174444 ENSG00000137818 ENSG00000182774 ENSG00000140986
## "RPS27L" "RPL4" "RPLP1" "RPS17" "RPL3L"
## ENSG00000140988 ENSG00000134419 ENSG00000167526 ENSG00000161970 ENSG00000198242
## "RPS2" "RPS15A" "RPL13" "RPL26" "RPL23A"
## ENSG00000125691 ENSG00000108298 ENSG00000131469 ENSG00000108443 ENSG00000172809
## "RPL23" "RPL19" "RPL27" "RPS6KB1" "RPL38"
## ENSG00000265681 ENSG00000115268 ENSG00000130255 ENSG00000233927 ENSG00000105640
## "RPL17" "RPS15" "RPL36" "RPS28" "RPL18A"
## ENSG00000105193 ENSG00000105372 ENSG00000063177 ENSG00000142541 ENSG00000142534
## "RPS16" "RPS19" "RPL18" "RPL13A" "RPS11"
## ENSG00000170889 ENSG00000108107 ENSG00000083845 ENSG00000171863 ENSG00000143947
## "RPS9" "RPL28" "RPS5" "RPS7" "RPS27A"
## ENSG00000071082 ENSG00000197756 ENSG00000171858 ENSG00000100316 ENSG00000187051
## "RPL31" "RPL37A" "RPS21" "RPL3" "RPS19BP1"
## ENSG00000144713 ENSG00000174748 ENSG00000168028 ENSG00000188846 ENSG00000162244
## "RPL32" "RPL15" "RPSA" "RPL14" "RPL29"
## ENSG00000114391 ENSG00000163584 ENSG00000163923 ENSG00000182899 ENSG00000163682
## "RPL24" "RPL22L1" "RPL39L" "RPL35A" "RPL9"
## ENSG00000109475 ENSG00000145425 ENSG00000145592 ENSG00000186468 ENSG00000164587
## "RPL34" "RPS3A" "RPL37" "RPS23" "RPS14"
## ENSG00000037241 ENSG00000231500 ENSG00000124614 ENSG00000198755 ENSG00000146223
## "RPL26L1" "RPS18" "RPS10" "RPL10A" "RPL7L1"
## ENSG00000112306 ENSG00000071242 ENSG00000008988 ENSG00000147604 ENSG00000156482
## "RPS12" "RPS6KA2" "RPS20" "RPL7" "RPL30"
## ENSG00000161016 ENSG00000137154 ENSG00000136942 ENSG00000197958 ENSG00000148303
## "RPL8" "RPS6" "RPL35" "RPL12" "RPL7A"
## ENSG00000177189 ENSG00000198034 ENSG00000072133 ENSG00000241343 ENSG00000198918
## "RPS6KA3" "RPS4X" "RPS6KA6" "RPL36A" "RPL39"
## ENSG00000147403 ENSG00000129824
## "RPL10" "RPS4Y1"Quick search for mitochondrial protein ATP8, which is also called MT-ATP8, shows that the name does not contain “MT-.” However, the correct feature (ENSEMBL ID ENSG00000228253) is present in our annotation.
grep("ATP8",rowData(umi)$SYMBOL,value = T)## ENSG00000143515 ENSG00000132932 ENSG00000104043 ENSG00000081923 ENSG00000130270
## "ATP8B2" "ATP8A2" "ATP8B4" "ATP8B1" "ATP8B3"
## ENSG00000124406 ENSG00000228253
## "ATP8A1" "ATP8"Most modern annotations, e.g. ones used by Cell Ranger, will have mitochondrial genes names that start with MT-. For some reason, the one we have found does not. Annotation problems in general are very common and should be always considered carefully. In our case, we also can’t find the location of genes since chromosomes are not supported in org.Hs.eg.db - there are no genome location columns in this database:
columns(org.Hs.eg.db)## [1] "ACCNUM" "ALIAS" "ENSEMBL" "ENSEMBLPROT" "ENSEMBLTRANS"
## [6] "ENTREZID" "ENZYME" "EVIDENCE" "EVIDENCEALL" "GENENAME"
## [11] "GENETYPE" "GO" "GOALL" "IPI" "MAP"
## [16] "OMIM" "ONTOLOGY" "ONTOLOGYALL" "PATH" "PFAM"
## [21] "PMID" "PROSITE" "REFSEQ" "SYMBOL" "UCSCKG"
## [26] "UNIPROT"Let’s try a different, more detailed database - EnsDb.Hsapiens.v86. Using this resource, we can find 13 protein-coding genes located in the mitochondrion:
ensdb_genes <- genes(EnsDb.Hsapiens.v86)
MT_names <- ensdb_genes[seqnames(ensdb_genes) == "MT"]$gene_id
is_mito <- rownames(umi) %in% MT_names
table(is_mito)## is_mito
## FALSE TRUE
## 18065 136.1.3 Basic QC
The following scater functions allow us to add per-cell and per-gene metrics useful for dataset evaluation. Most popular metrics per cell are total number of counts (UMIs), total number of detected genes, total number of mitochondrial counts, percent of mitochondrial counts, etc.
umi_cell <- perCellQCMetrics(umi,subsets=list(Mito=is_mito))
umi_feature <- perFeatureQCMetrics(umi)
head(umi_cell)## DataFrame with 6 rows and 9 columns
## sum detected subsets_Mito_sum subsets_Mito_detected
## <numeric> <numeric> <numeric> <numeric>
## NA19098.r1.A01 61707 8242 4883 13
## NA19098.r1.A02 62300 8115 3732 13
## NA19098.r1.A03 42212 7189 3089 13
## NA19098.r1.A04 52324 7863 3606 13
## NA19098.r1.A05 69192 8494 4381 13
## NA19098.r1.A06 66341 8535 3235 13
## subsets_Mito_percent altexps_ERCC_sum altexps_ERCC_detected
## <numeric> <numeric> <numeric>
## NA19098.r1.A01 7.91320 1187 31
## NA19098.r1.A02 5.99037 1277 31
## NA19098.r1.A03 7.31782 1121 28
## NA19098.r1.A04 6.89167 1240 30
## NA19098.r1.A05 6.33166 1262 33
## NA19098.r1.A06 4.87632 1308 30
## altexps_ERCC_percent total
## <numeric> <numeric>
## NA19098.r1.A01 1.88730 62894
## NA19098.r1.A02 2.00859 63577
## NA19098.r1.A03 2.58694 43333
## NA19098.r1.A04 2.31499 53564
## NA19098.r1.A05 1.79124 70454
## NA19098.r1.A06 1.93351 67649head(umi_feature)## DataFrame with 6 rows and 2 columns
## mean detected
## <numeric> <numeric>
## ENSG00000187634 0.0300926 2.77778
## ENSG00000188976 2.6388889 84.25926
## ENSG00000187961 0.2384259 20.60185
## ENSG00000187583 0.0115741 1.15741
## ENSG00000187642 0.0127315 1.27315
## ENSG00000188290 0.0243056 2.31481We can now use the functions that add the metrics calculated above to per-cell and per-gene metadata:
umi <- addPerCellQC(umi, subsets=list(Mito=is_mito))
umi <- addPerFeatureQC(umi)Manual filtering can use any cutoff we choose. In order to find a good value, it’s good to look at the distribution:
hist(
umi$total,
breaks = 100
)
abline(v = 25000, col = "red")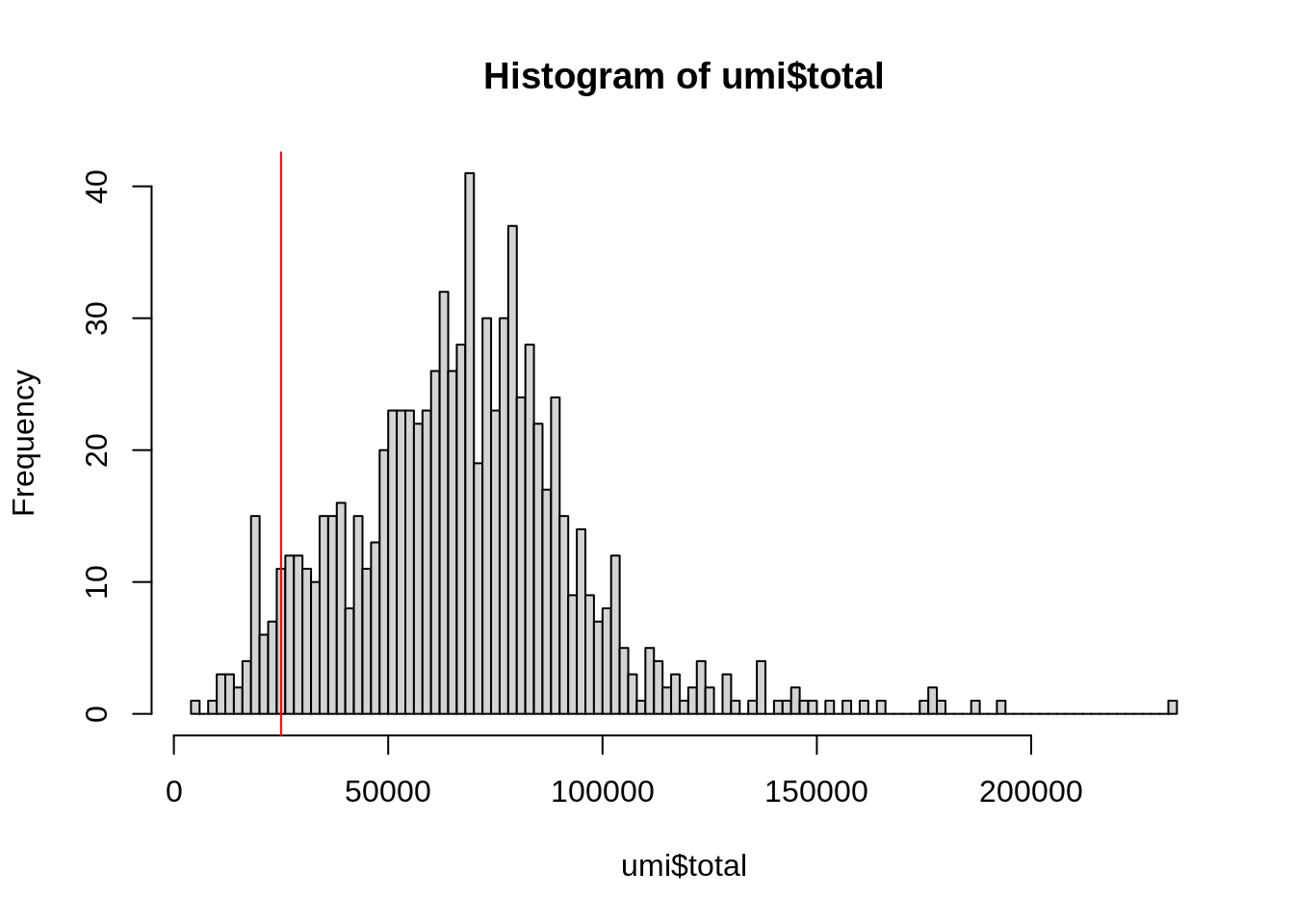
hist(
umi_cell$detected,
breaks = 100
)
abline(v = 7000, col = "red")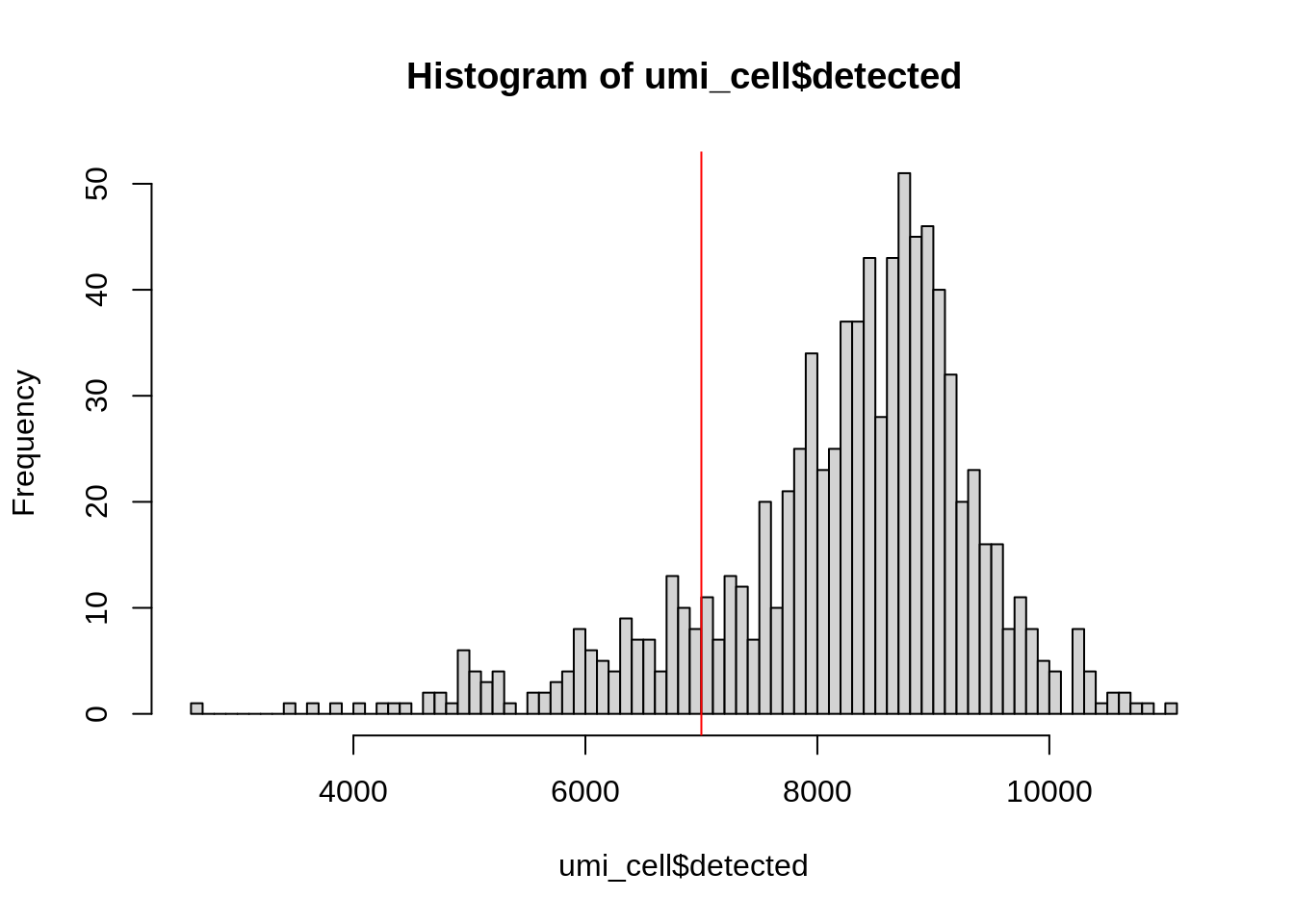
Sometimes it’s hard to come up with an obvious filtering cutoff. In this case, adaptive threshold can help us identify points that are more than 3 median absolute deviations (MADs) away from the median in any of the variables we use for QC. Be careful to specify if the correct direction of the deviation: indeed, low number of detected genes, but high MT gene percentage, are hallmarks of a low quality cell:
qc.lib2 <- isOutlier(umi_cell$sum, log=TRUE, type="lower")
attr(qc.lib2, "thresholds")## lower higher
## 23588.23 Infqc.nexprs2 <- isOutlier(umi_cell$detected, log=TRUE, type="lower")
attr(qc.nexprs2, "thresholds")## lower higher
## 6252.451 Infqc.spike2 <- isOutlier(umi_cell$altexps_ERCC_percent, type="higher")
attr(qc.spike2, "thresholds")## lower higher
## -Inf 3.619558qc.mito2 <- isOutlier(umi_cell$subsets_Mito_percent, type="higher")
attr(qc.mito2, "thresholds")## lower higher
## -Inf 9.294928discard2 <- qc.lib2 | qc.nexprs2 | qc.spike2 | qc.mito2
DataFrame(LibSize=sum(qc.lib2), NExprs=sum(qc.nexprs2), SpikeProp=sum(qc.spike2), MitoProp=sum(qc.mito2), Total=sum(discard2))## DataFrame with 1 row and 5 columns
## LibSize NExprs SpikeProp MitoProp Total
## <integer> <integer> <integer> <integer> <integer>
## 1 47 65 137 75 194All the actions performed above could be done in one scater command, quickPerCellQC:
reasons <- quickPerCellQC(umi_cell, sub.fields=c("subsets_Mito_percent", "altexps_ERCC_percent"))
colSums(as.matrix(reasons))## low_lib_size low_n_features high_subsets_Mito_percent
## 47 65 75
## high_altexps_ERCC_percent discard
## 137 194Let’s add another metadata column that would keep the information about whether a cell is discarded or not:
umi$discard <- reasons$discardPlotting various coldata (cell-level medadata) assays against each other allows us to illustrate the dependencies between them. For example, cells with high mitochondrial content usually are considered dead or dying; these cells also usually have low overall UMI counts and number of detected genes.
plotColData(umi, x="sum", y="subsets_Mito_percent", colour_by="discard")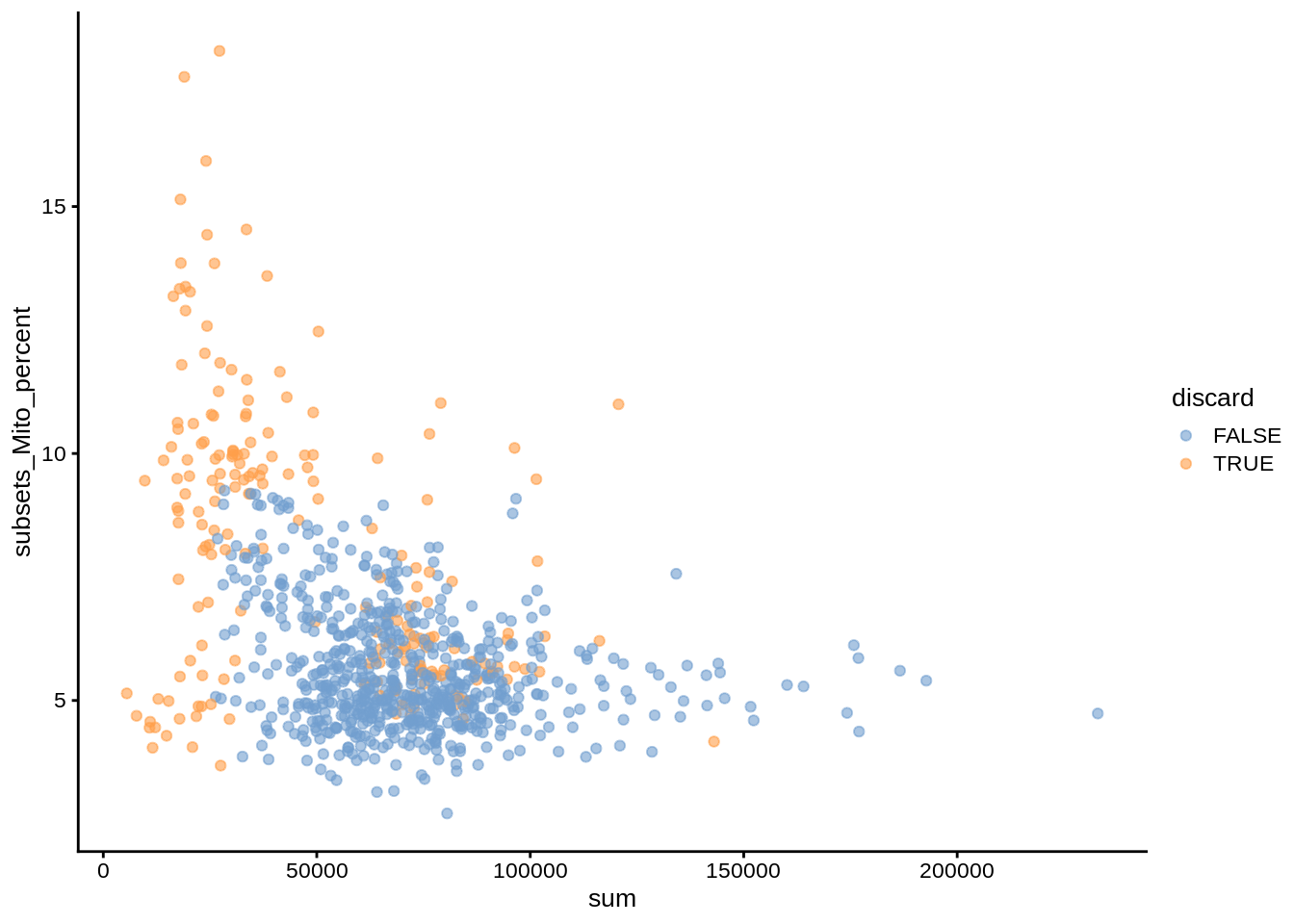
plotColData(umi, x="sum", y="detected", colour_by="discard")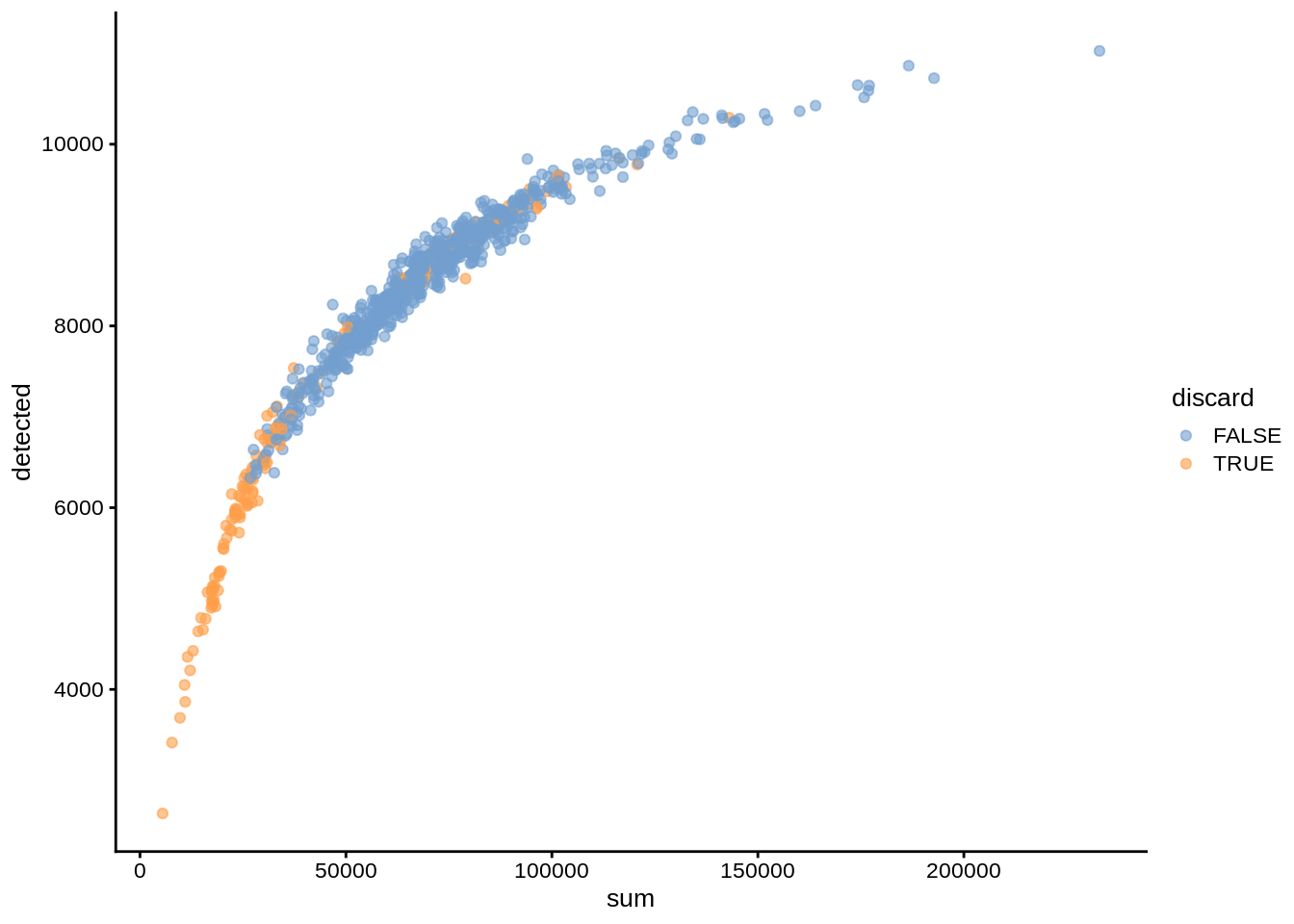
plotColData(umi, x="altexps_ERCC_percent", y="subsets_Mito_percent",colour_by="discard")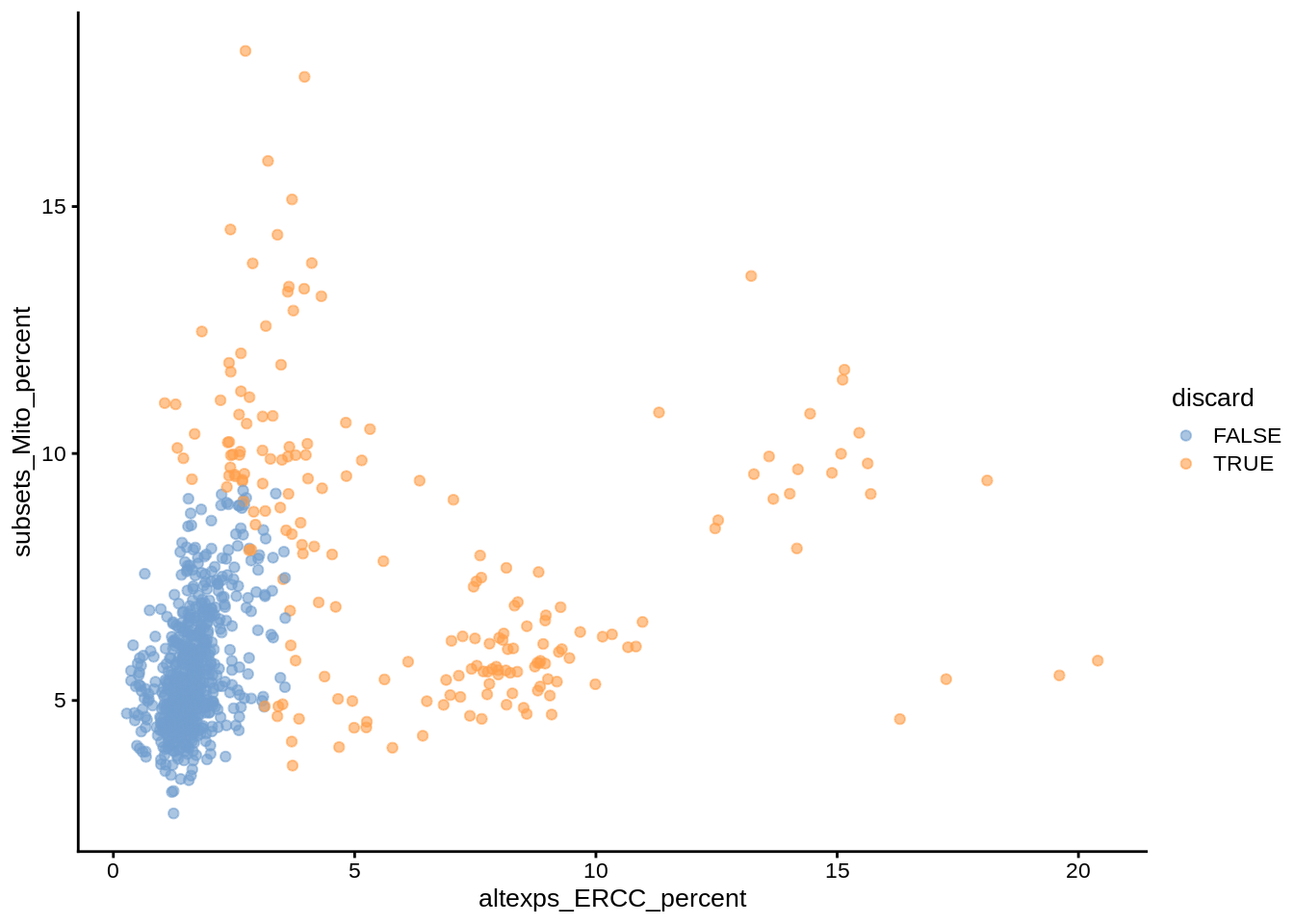
We can also plot coldata with splitting by batches to see if there are substantial batch-specific differences:
library(scales)
plotColData(umi, x="sum", y="detected", colour_by="discard", other_fields = "individual") +
facet_wrap(~individual) + scale_x_continuous(labels = unit_format(unit = "k", scale = 1e-3))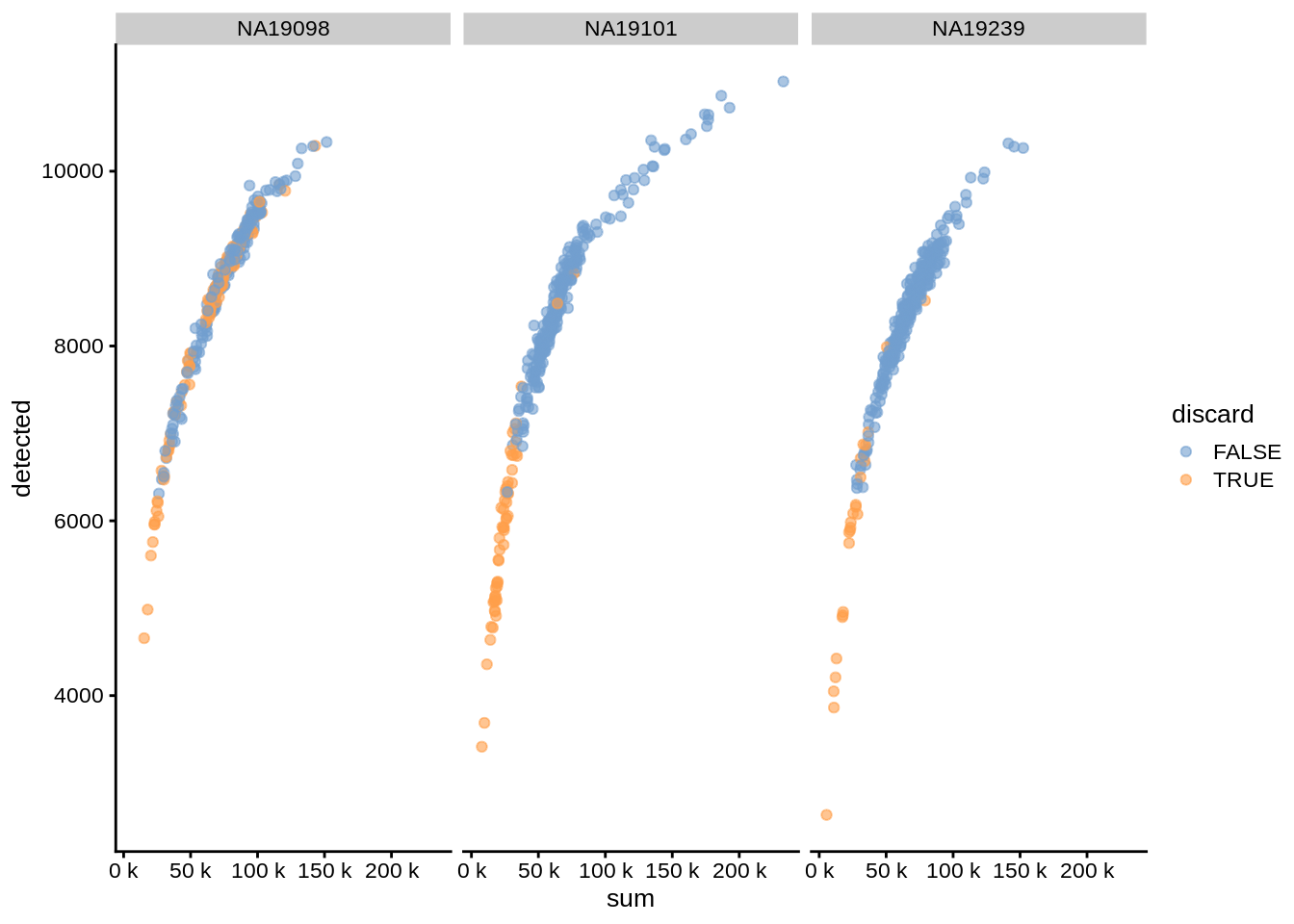
plotColData(umi, x="sum", y="detected", colour_by="discard", other_fields = "replicate") +
facet_wrap(~replicate) + scale_x_continuous(labels = unit_format(unit = "k", scale = 1e-3))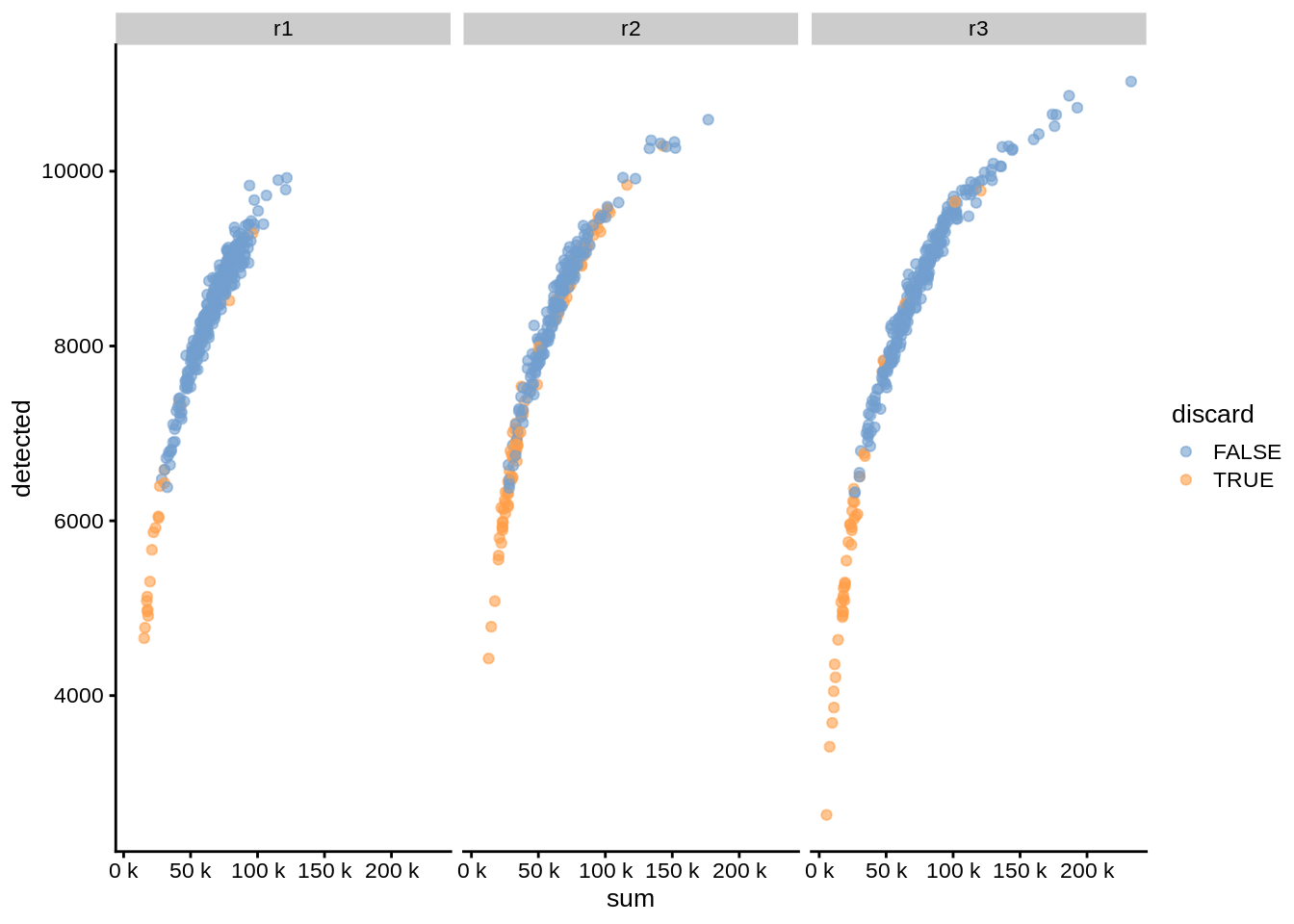
6.1.4 Highly Expressed Genes
Let’s take a look at the most expressed genes in the whole dataset. We will use symbols we obtained above. Most of the genes we see are mitochondrial or ribosomal proteins, which is pretty typical for most scRNA-seq datasets.
plotHighestExprs(umi, exprs_values = "counts",
feature_names_to_plot = "SYMBOL", colour_cells_by="detected")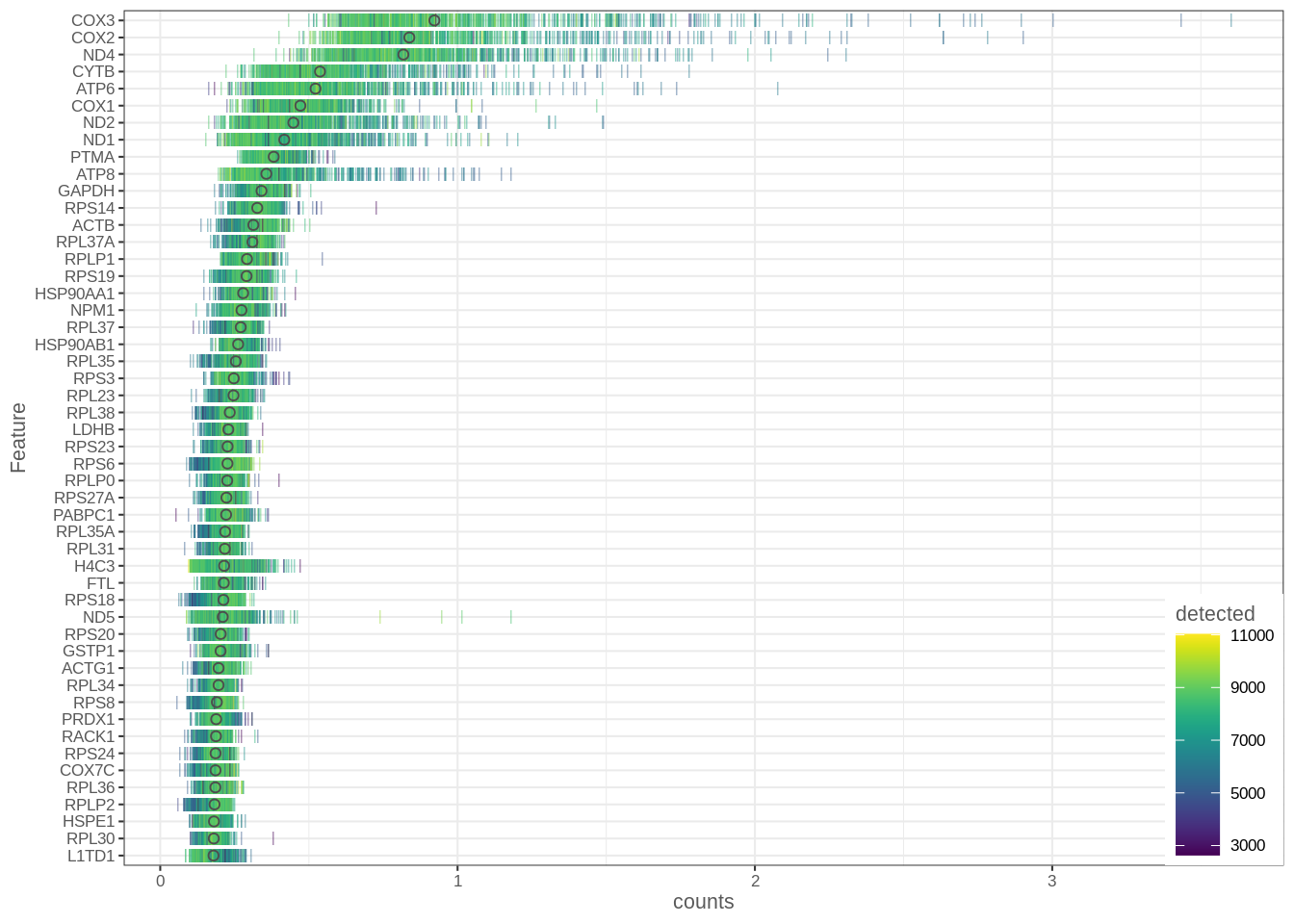
Let’s keep the genes which were detected (expression value > 1) in 2 or more cells. We’ll discard approximately 4,000 weakly expressed genes.
keep_feature <- nexprs(umi,byrow = TRUE,detection_limit = 1) >= 2
rowData(umi)$discard <- ! keep_feature
table(rowData(umi)$discard)##
## FALSE TRUE
## 13873 4205Let’s make a new assay, logcounts_raw, which will contain log2-transformed counts with added pseudocount of 1.
assay(umi, "logcounts_raw") <- log2(counts(umi) + 1)Finally, let’s save the SingleCellExperiment object with all the fields we have added to the per-cell metadata, and new assays (logcounts_raw):
saveRDS(umi, file = "data/tung/umi.rds")6.2 Data Visualization and Dimensionality Reduction
6.2.1 Introduction
In this chapter we will continue to work with the filtered Tung dataset produced in the previous chapter. We will explore different ways of visualizing the data to allow you to asses what happened to the expression matrix after the quality control step. scater package provides several very useful functions to simplify visualisation.
One important aspect of single-cell RNA-seq is to control for batch effects. Batch effects are technical artefacts that are added to the samples during handling. For example, if two sets of samples were prepared in different labs or even on different days in the same lab, then we may observe greater similarities between the samples that were handled together. In the worst case scenario, batch effects may be mistaken for true biological variation. The Tung data allows us to explore these issues in a controlled manner since some of the salient aspects of how the samples were handled have been recorded. Ideally, we expect to see batches from the same individual grouping together and distinct groups corresponding to each individual.
Let’s create another SingleCellExperiment object, umi.qc, in which remove unnecessary poorly expressed genes and low quality cells.
umi.qc <- umi[! rowData(umi)$discard,! colData(umi)$discard]6.2.2 PCA plot
The easiest way to overview the data is by transforming it using the principal component analysis and then visualize the first two principal components.
Principal component analysis (PCA) is a statistical procedure that uses a transformation to convert a set of observations into a set of linearly uncorrelated (orthogonal) variables called principal components (PCs). The number of principal components is less than or equal to the number of original variables.
Mathematically, the PCs correspond to the eigenvectors of the covariance matrix. The eigenvectors are sorted by eigenvalue so that the first principal component accounts for as much of the variability in the data as possible, and each succeeding component in turn has the highest variance possible under the constraint that it is orthogonal to the preceding components (the figure below is taken from here).
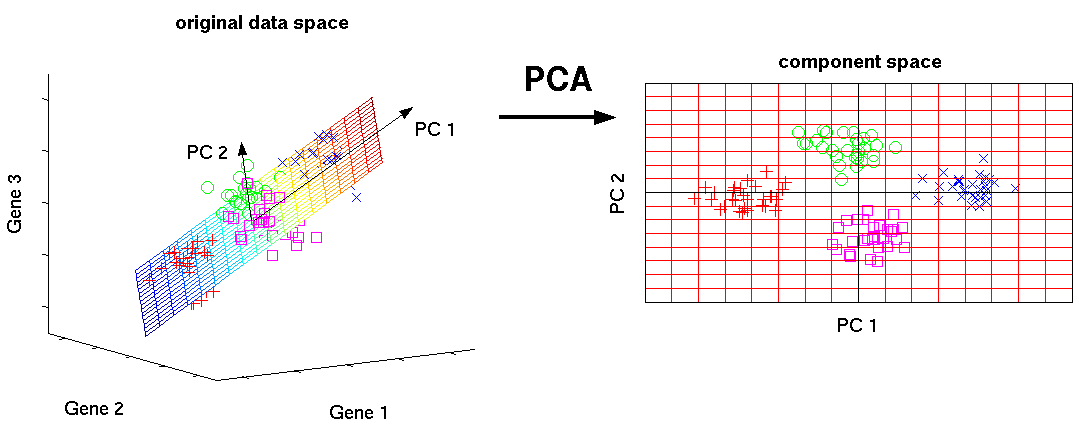
Figure 6.1: Schematic representation of PCA dimensionality reduction
6.2.2.1 Before QC
Without log-transformation or normalization, PCA plot fails to separate the datasets by replicate or individual. We mostly see the effects of sequencing depth - samples (cells) with lots of expression, and particularly highly expressed genes, dominate the PCs:
umi <- runPCA(umi, exprs_values = "counts")
dim(reducedDim(umi, "PCA"))## [1] 864 50plotPCA(umi, colour_by = "batch", size_by = "detected", shape_by = "individual")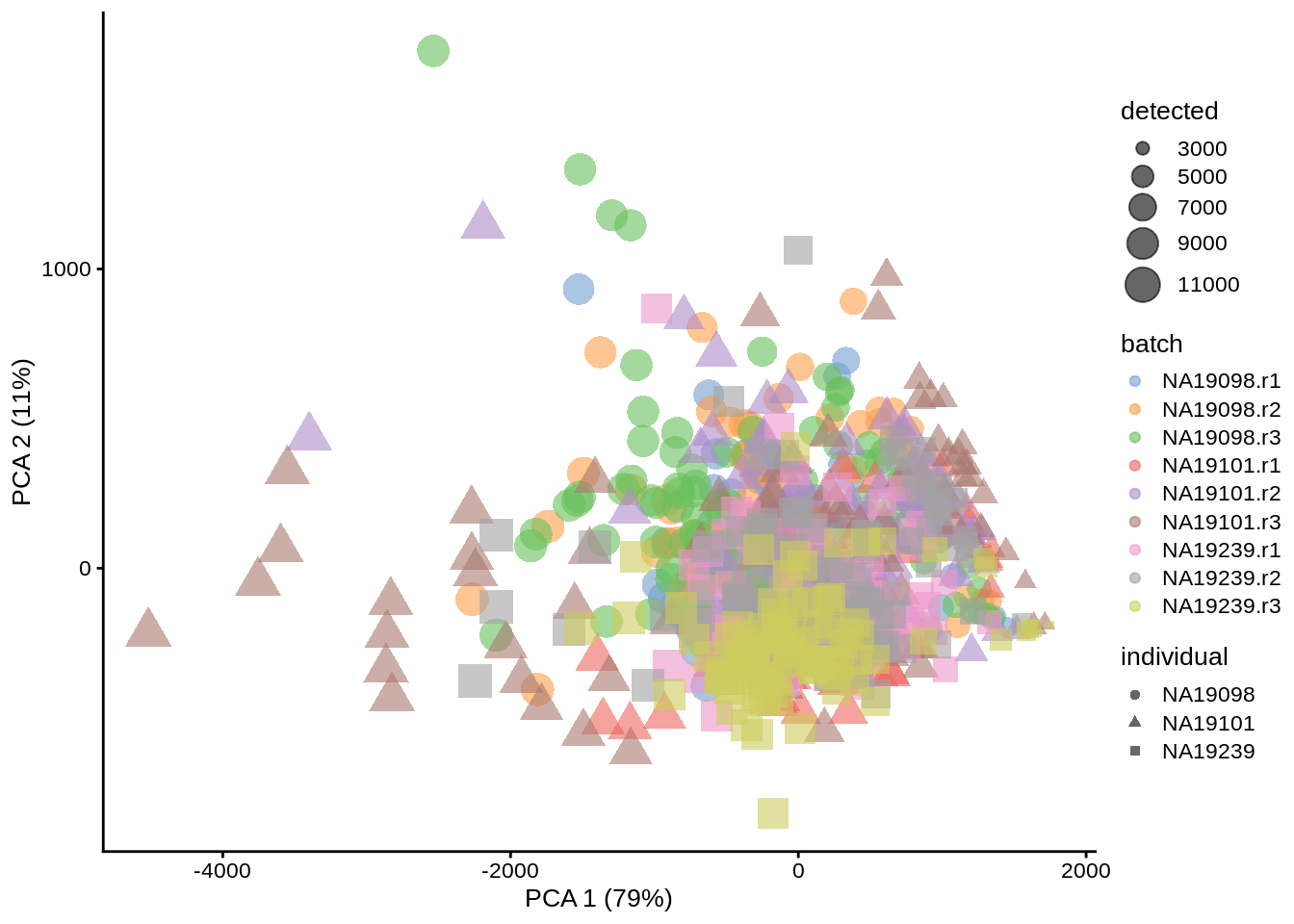
Figure 6.2: PCA plot of the Tung data (raw counts)
With log-transformation, we equalize the large difference between strongly and weakly expressed genes, and immediately see cells form groups by replicate, individual, and sequencing depth. When PCA is re-run, reducedDim object in umi is overwritten.
umi <- runPCA(umi, exprs_values = "logcounts_raw")
dim(reducedDim(umi, "PCA"))## [1] 864 50plotPCA(umi, colour_by = "batch", size_by = "detected", shape_by = "individual")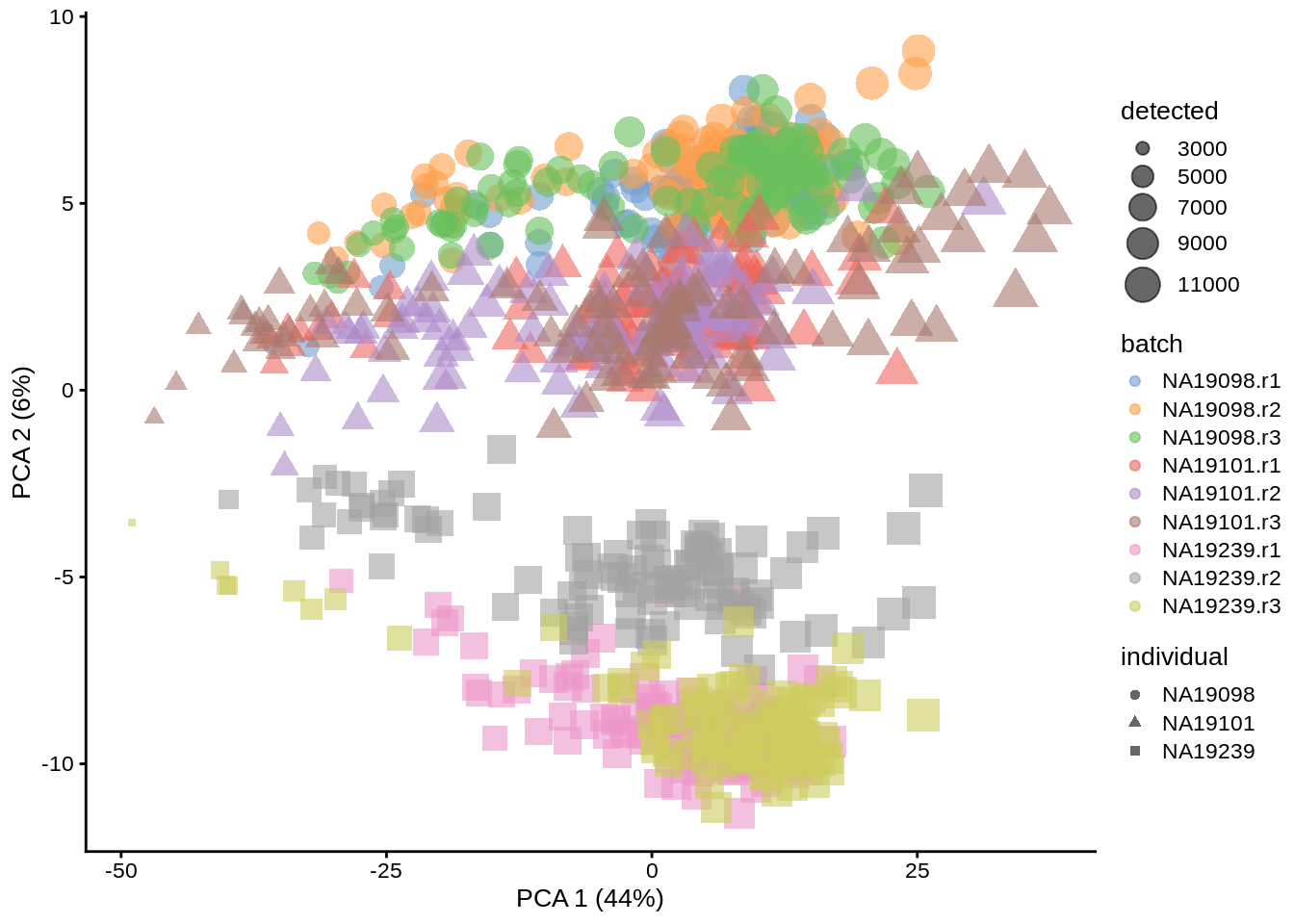
Figure 6.3: PCA plot of the tung data (non-normalized logcounts)
Clearly log-transformation is benefitial for our data - it reduces the variance on the first principal component and already separates some biological effects. Moreover, it makes the distribution of the expression values more normal. In the following analysis and chapters we will be using log-transformed raw counts by default.
However, note that just a log-transformation is not enough to account for different technical factors between the cells (e.g. sequencing depth). Therefore, please do not use logcounts_raw for your downstream analysis, instead as a minimum suitable data use the logcounts slot of the SingleCellExperiment object, which not just log-transformed, but also normalised by library size (e.g. CPM normalisation). In the course we use logcounts_raw only for demonstration purposes!
6.2.2.2 After QC
Let’s do the same analysis as above, but using umi.qc dataframe instead of the full umi:
umi.qc <- runPCA(umi.qc, exprs_values = "logcounts_raw")
dim(reducedDim(umi.qc, "PCA"))## [1] 670 50plotPCA(umi.qc, colour_by = "batch", size_by = "detected", shape_by = "individual")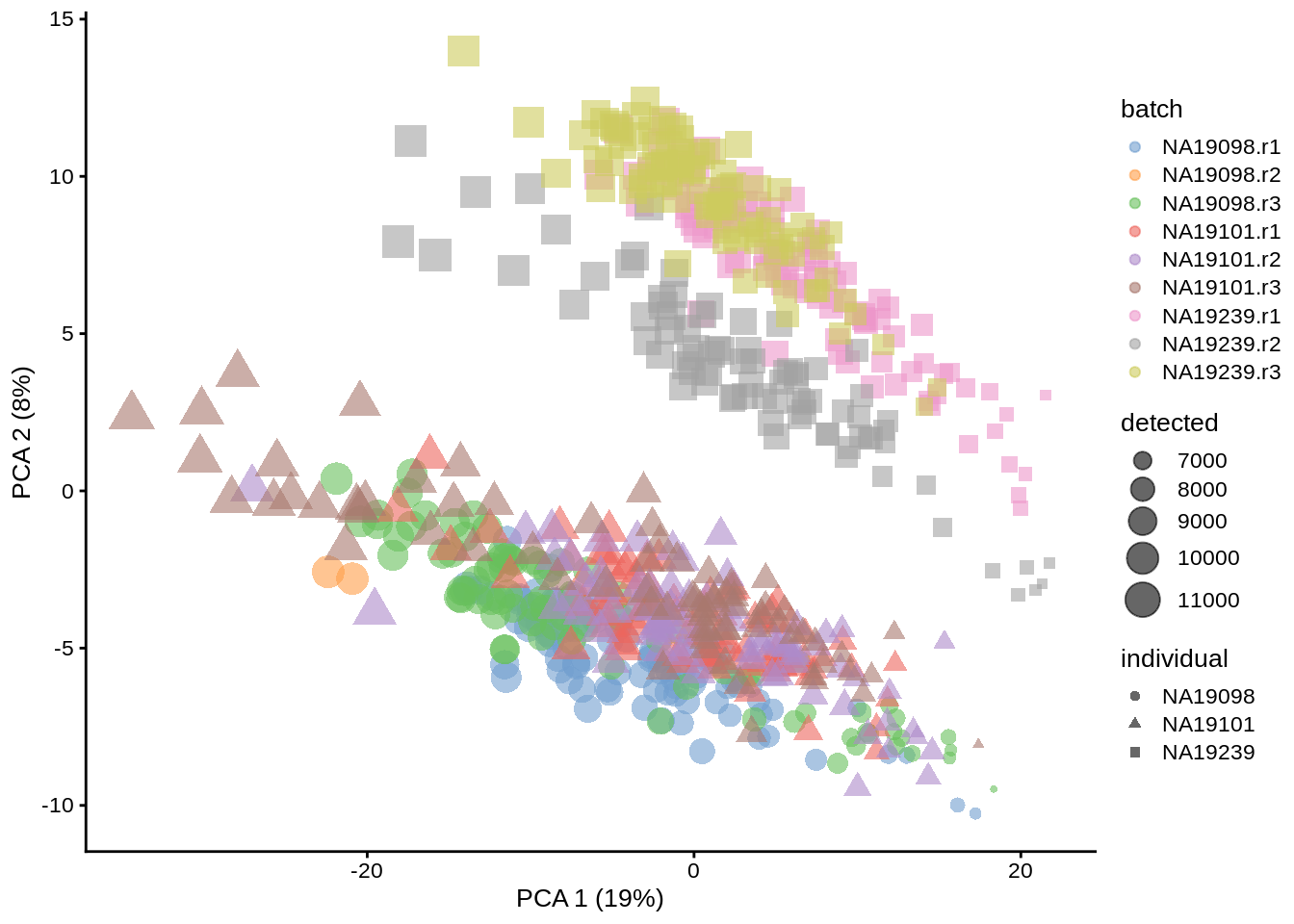
Figure 6.4: PCA plot of the Tung data (non-normalized log counts, QC-filtered)
Comparing figures above, it is clear that after quality control the NA19098.r2 cells no longer form a group of outliers.
By default only the top 500 most variable genes are used by scater to calculate the PCA. This can be adjusted by changing the ntop argument.
Exercise 1 How do the PCA plots change if when all 14,154 genes are used? Or when only top 50 genes are used? Why does the fraction of variance accounted for by the first PC change so dramatically?
Hint Use ntop argument of the plotPCA function.
Answer
umi.qc <- runPCA(umi.qc, exprs_values = "logcounts_raw",ntop = nrow(umi.qc))
plotPCA(umi.qc, colour_by = "batch", size_by = "detected", shape_by = "individual")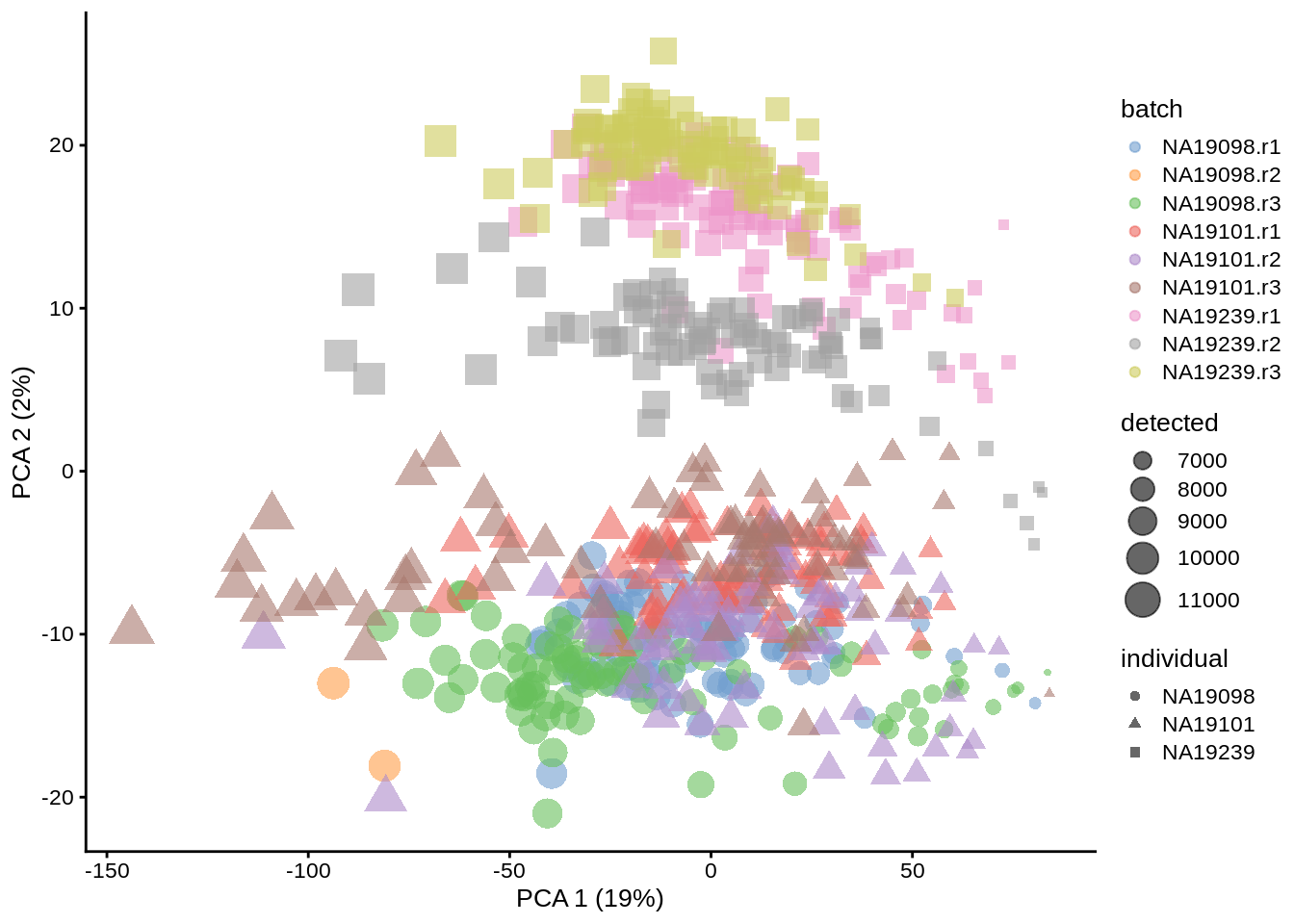
Figure 6.5: PCA plot of the tung data (14214 genes)
umi.qc <- runPCA(umi.qc, exprs_values = "logcounts_raw",ntop = 50)## Warning in check_numbers(k = k, nu = nu, nv = nv, limit = min(dim(x)) - : more
## singular values/vectors requested than available## Warning in (function (A, nv = 5, nu = nv, maxit = 1000, work = nv + 7, reorth =
## TRUE, : You're computing too large a percentage of total singular values, use a
## standard svd instead.## Warning in (function (A, nv = 5, nu = nv, maxit = 1000, work = nv + 7, reorth
## = TRUE, : did not converge--results might be invalid!; try increasing work or
## maxitplotPCA(umi.qc, colour_by = "batch", size_by = "detected", shape_by = "individual")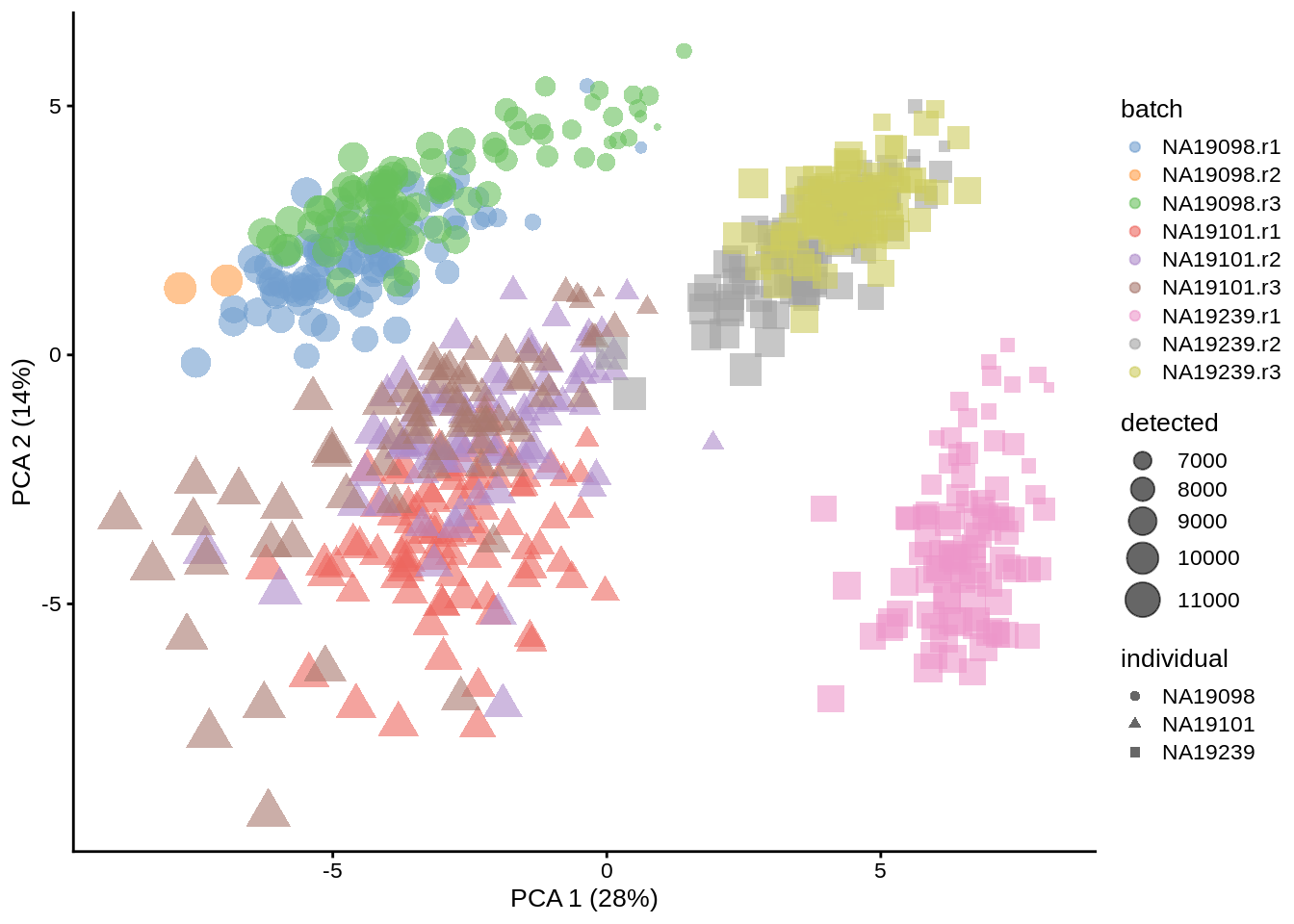
(#fig:exprs-over7, expr-overview-pca-after-qc-exercise1-2)PCA plot of the tung data (50 genes)
6.2.3 tSNE Map
An alternative to PCA for visualizing scRNA-seq data is a tSNE plot. tSNE (t-Distributed Stochastic Neighbor Embedding) combines dimensionality reduction (e.g. PCA) with random walks on the nearest-neighbour network to map high dimensional data (i.e. our 14,154-dimensional expression matrix) to a 2-dimensional space while preserving local distances between cells. In contrast with PCA, tSNE is a stochastic algorithm which means running the method multiple times on the same dataset will result in different plots. Due to the non-linear and stochastic nature of the algorithm, tSNE is more difficult to intuitively interpret tSNE. To ensure reproducibility, we fix the “seed” of the random-number generator in the code below so that we always get the same plot.
6.2.3.1 Before QC
set.seed(123456)
umi <- runTSNE(umi, exprs_values = "logcounts_raw", perplexity = 130)
plotTSNE(umi, colour_by = "batch", size_by = "detected", shape_by = "individual")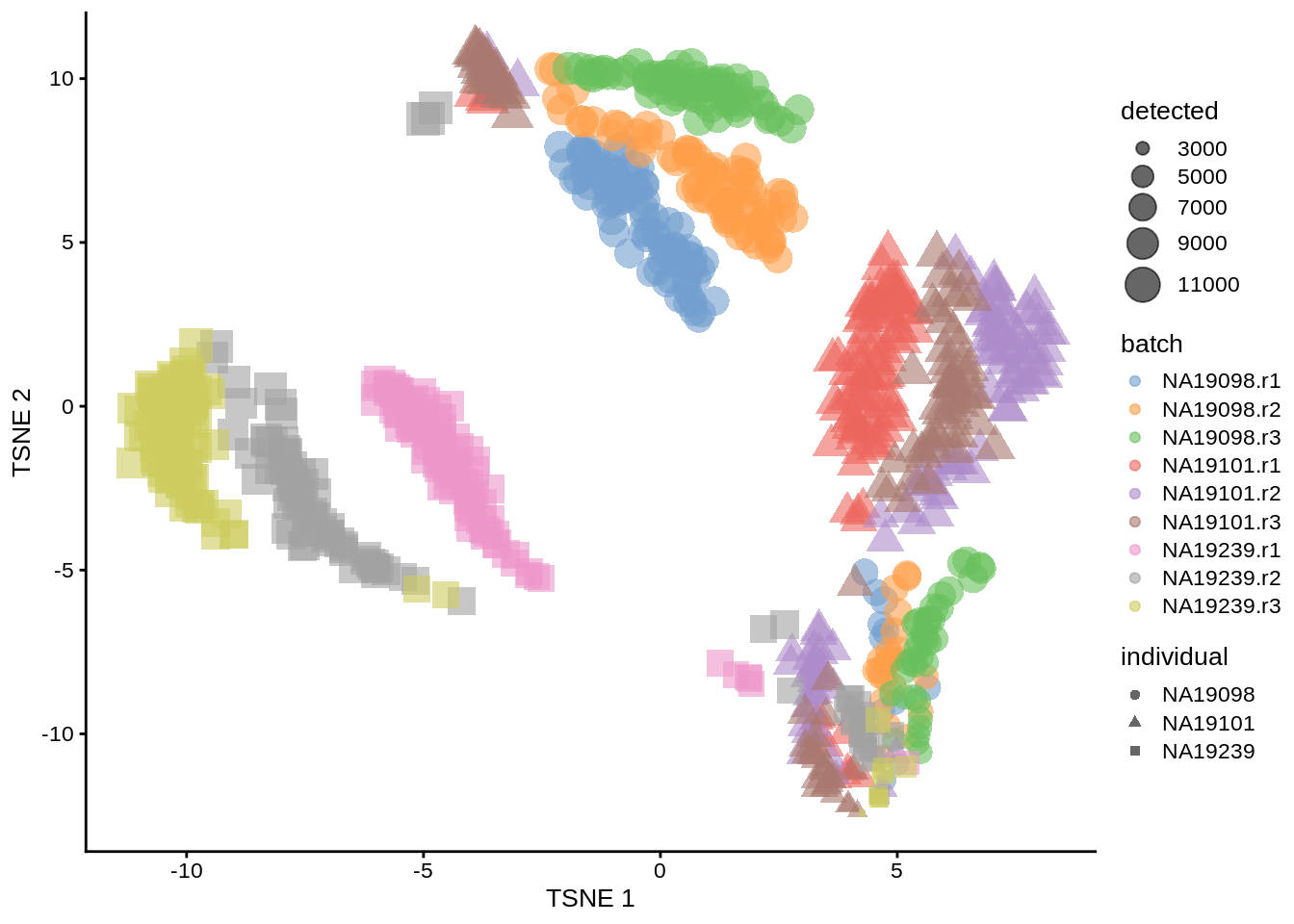
Figure 6.6: tSNE map of the tung data
6.2.3.2 After QC
set.seed(123456)
umi.qc <- runTSNE(umi.qc, exprs_values = "logcounts_raw", perplexity = 130)
plotTSNE(umi.qc, colour_by = "batch", size_by = "detected", shape_by = "individual")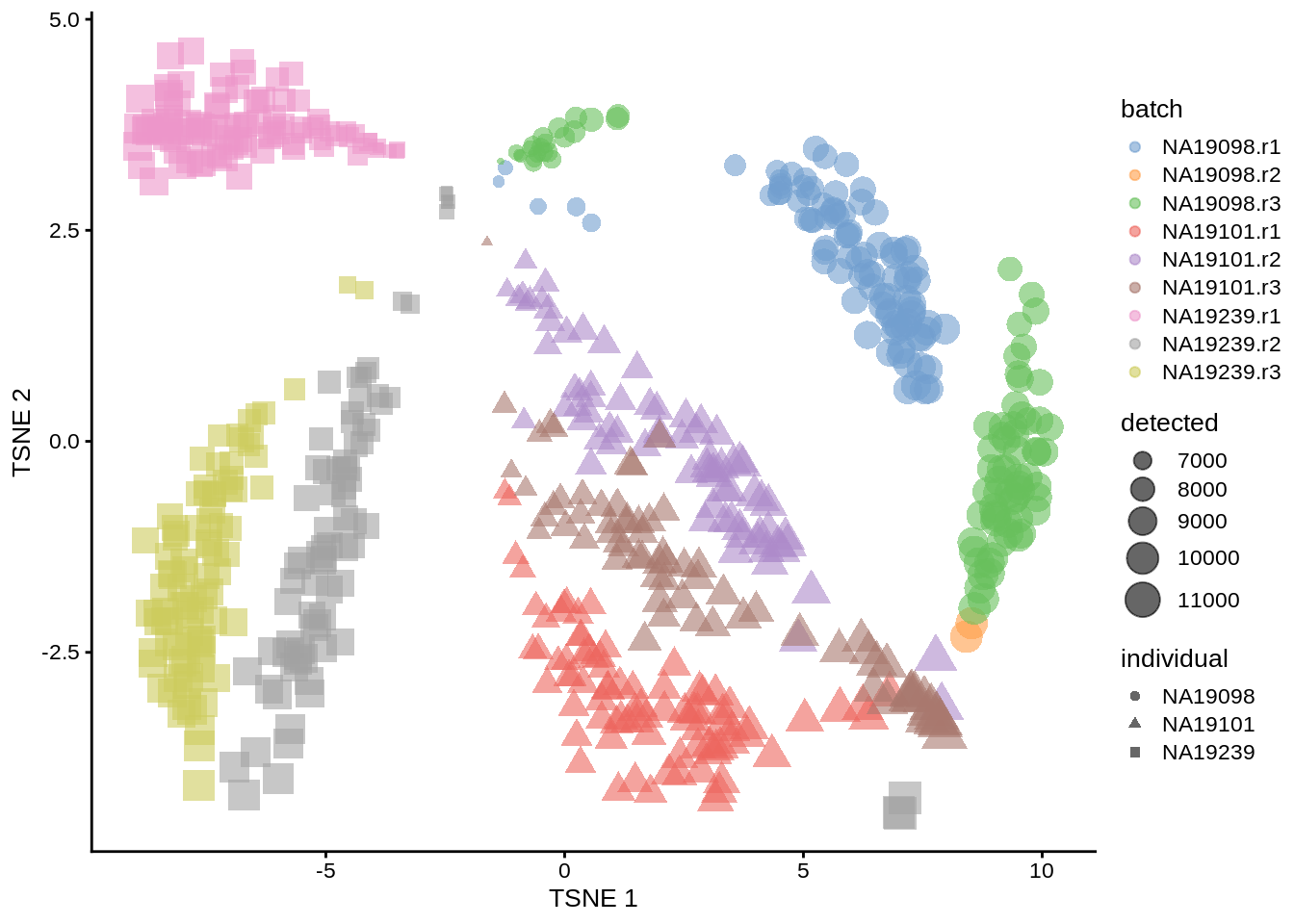
Figure 6.7: tSNE map of the tung data
Interpreting PCA and tSNE plots is often challenging and due to their stochastic and non-linear nature, they are less intuitive. However, in this case it is clear that they provide a similar picture of the data. Comparing figures above, it is again clear that the samples from NA19098.r2 are no longer outliers after the QC filtering.
Furthermore tSNE requires you to provide a value of perplexity which reflects the number of neighbours used to build the nearest-neighbour network; a high value creates a dense network which clumps cells together while a low value makes the network more sparse allowing groups of cells to separate from each other. scater uses a default perplexity of the total number of cells divided by five (rounded down).
You can read more about the pitfalls of using tSNE here. A more recent publication entitled “The art of using t-SNE for single-cell transcriptomics” discusses similarities and differences between t-SNE and UMAP, finding that most observed differences are due to initialization, and gives recommendataion on parameter tuning when visualizing scRNA-seq datasets of different sizes.
Exercise 2 How do the tSNE plots change when a perplexity of 10 or 200 is used? How does the choice of perplexity affect the interpretation of the results?
Answer
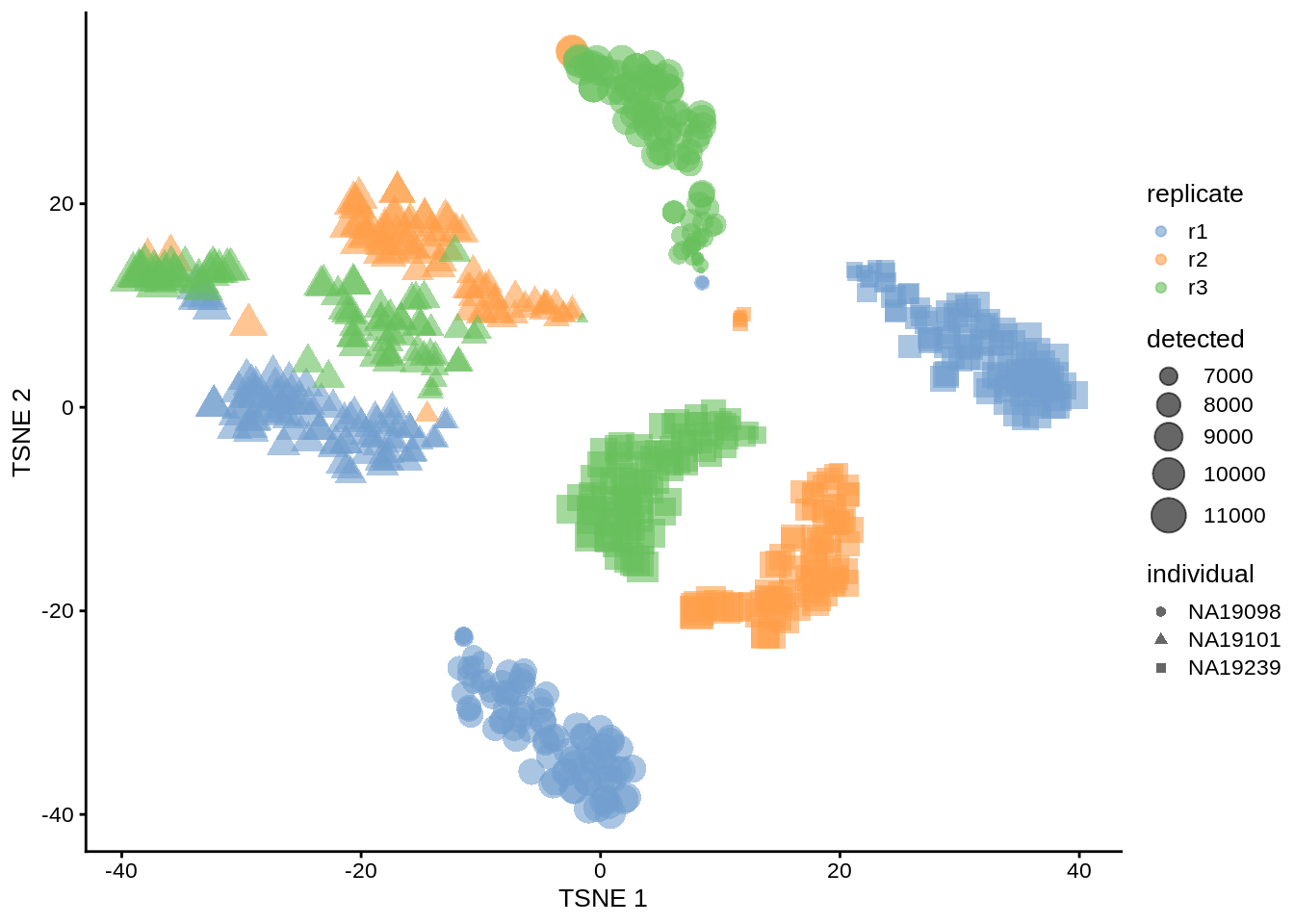
Figure 6.8: tSNE map of the tung data (perplexity = 10)
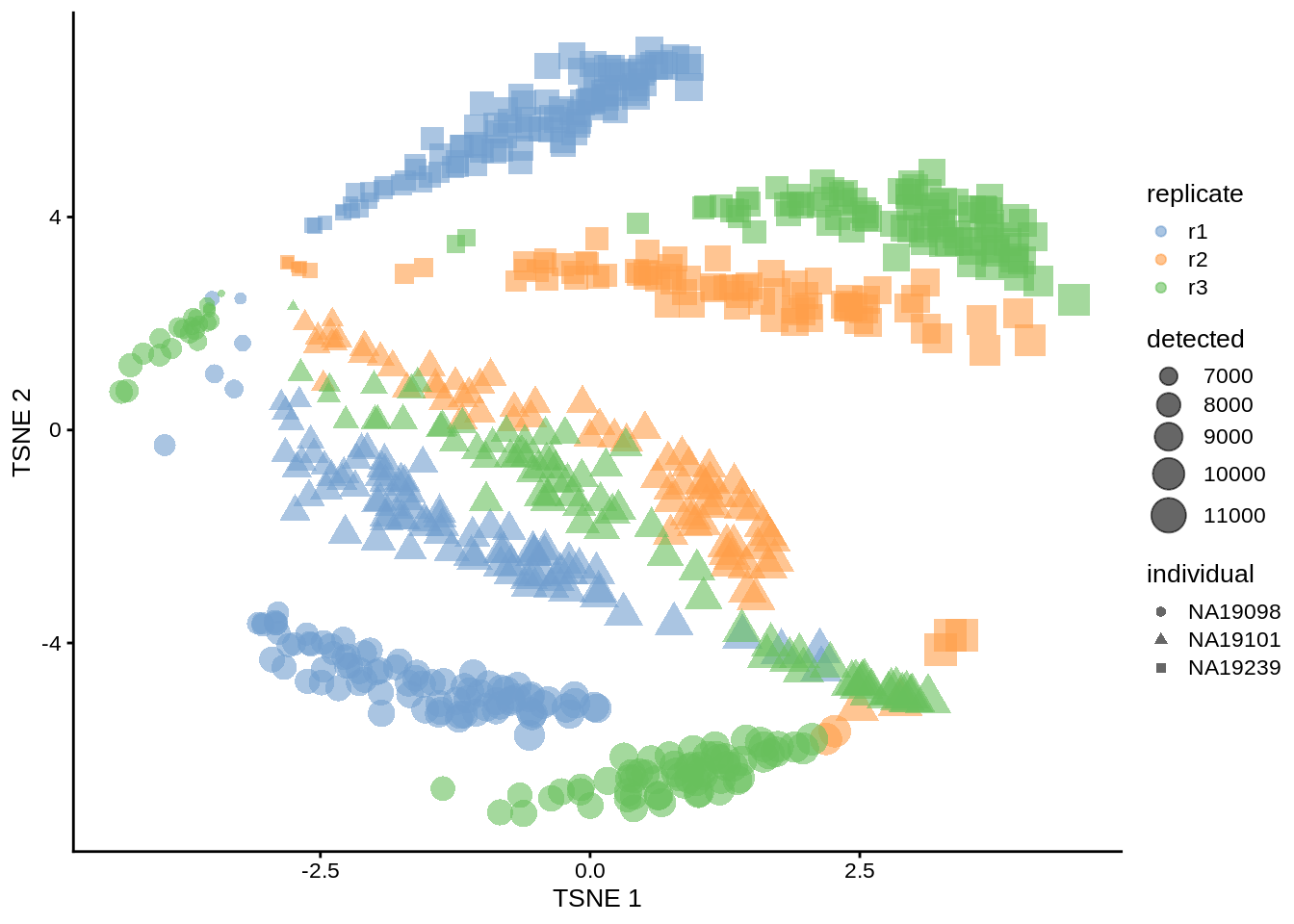
Figure 6.9: tSNE map of the tung data (perplexity = 200)
6.3 Identifying Confounding Factors
6.3.1 Introduction
There is a large number of potential confounders, artifacts and biases in scRNA-seq data. One of the main challenges in analyzing scRNA-seq data stems from the fact that it is difficult to carry out a true technical replicate (why?) to distinguish biological and technical variability. In the previous chapters we considered batch effects and in this chapter we will continue to explore how experimental artifacts can be identified and removed. We will continue using the scater package since it provides a set of methods specifically for quality control of experimental and explanatory variables. Moreover, we will continue to work with the Blischak data that was used in the previous chapter.
Our umi.qc dataset contains filtered cells and genes. Our next step is to explore technical drivers of variability in the data to inform data normalisation before downstream analysis.
6.3.2 Correlations with PCs
Let’s first look again at the PCA plot of the QC-filtered dataset:
umi.qc <- runPCA(umi.qc, exprs_values = "logcounts_raw")
dim(reducedDim(umi.qc, "PCA"))## [1] 670 50plotPCA(umi.qc, colour_by = "batch", size_by = "sum", shape_by = "individual")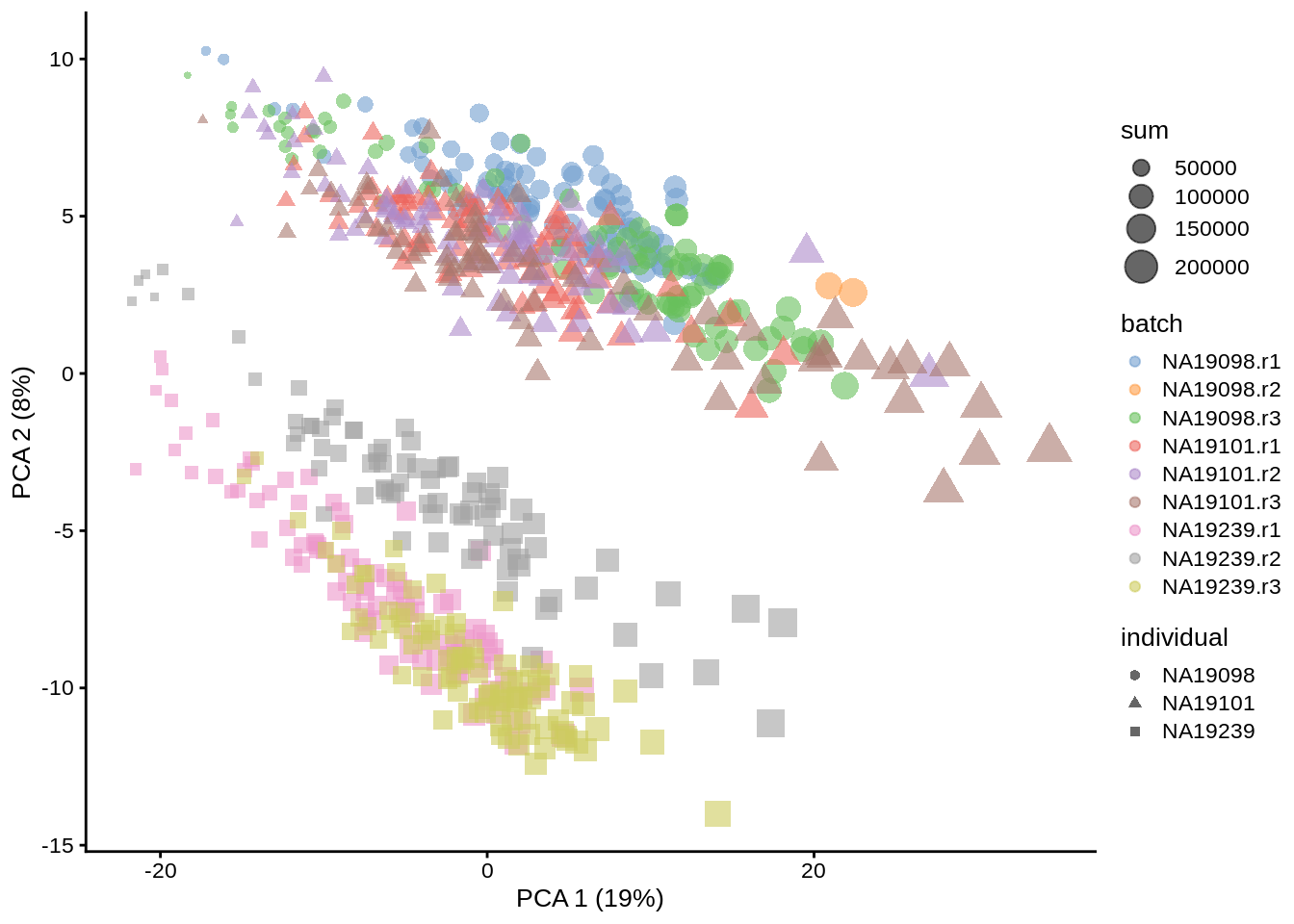
Figure 6.10: PCA plot of the tung data
scater allows one to identify principal components that correlate with experimental and QC variables of interest (it ranks principle components by \(R^2\) from a linear model regressing PC value against the variable of interest).
Let’s test whether some of the variables correlate with any of the PCs.
6.3.2.1 Detected genes
logcounts(umi.qc) <- assay(umi.qc, "logcounts_raw")
getExplanatoryPCs(umi.qc,variables = "sum")## sum
## PC1 8.663881e+01
## PC2 5.690790e+00
## PC3 1.709315e-01
## PC4 4.580131e-01
## PC5 1.923186e-04
## PC6 6.803561e-01
## PC7 1.057606e-01
## PC8 2.044205e-01
## PC9 5.652119e-01
## PC10 4.717890e-03plotExplanatoryPCs(umi.qc,variables = "sum") 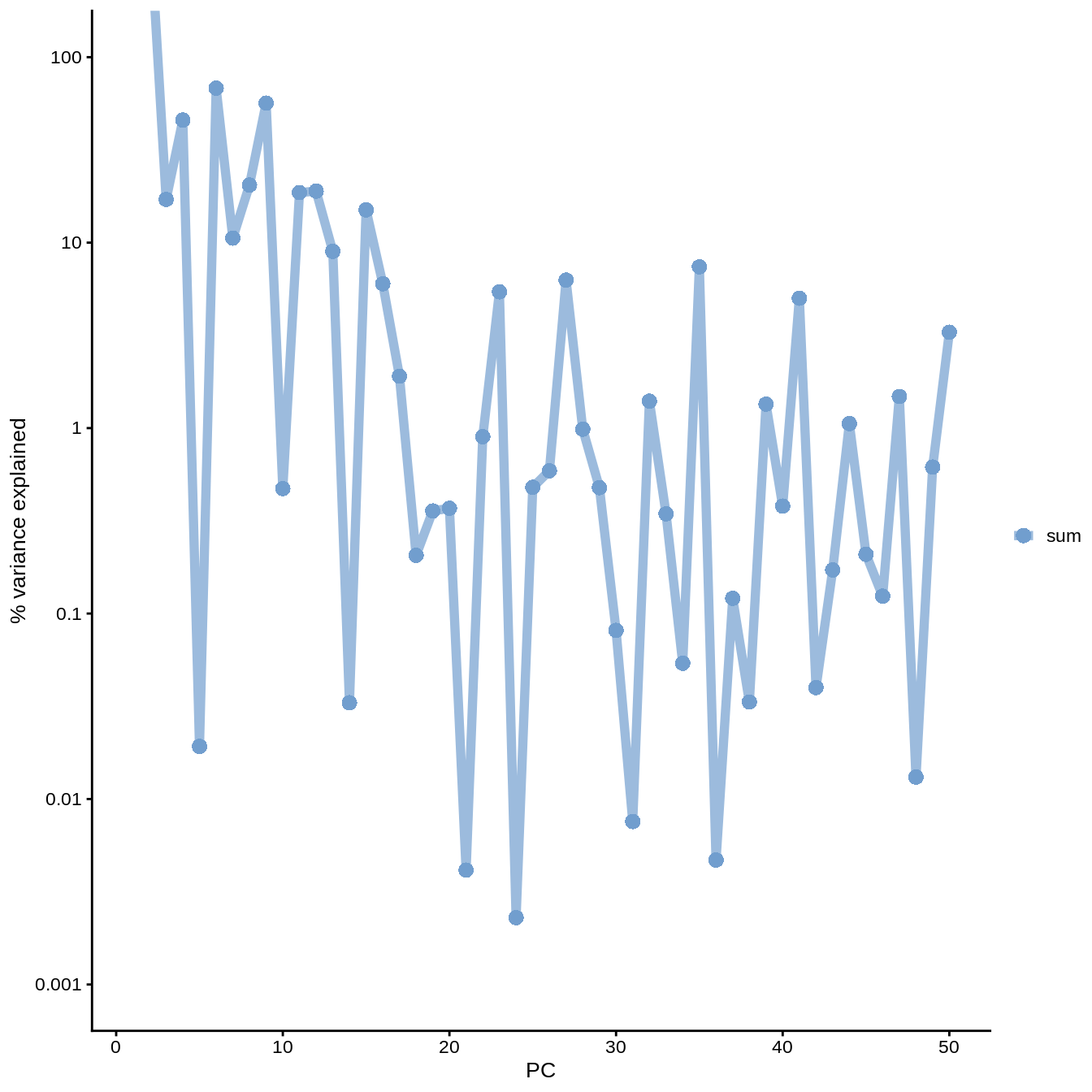
Figure 6.11: PC correlation with the number of detected genes
logcounts(umi.qc) <- NULLIndeed, we can see that PC1 can be almost completely (86%) explained by the total UMI counts (sequencing depth). In fact, it was also visible on the PCA plot above. This is a well-known issue in scRNA-seq and was described here.
6.3.3 Explanatory Variables
scater can also compute the marginal \(R^2\) for each variable when fitting a linear model regressing expression values for each gene against just that variable, and display a density plot of the gene-wise marginal \(R^2\) values for the variables.
plotExplanatoryVariables(umi.qc,exprs_values = "logcounts_raw",
variables = c("detected","sum","batch",
"individual","altexps_ERCC_percent","subsets_Mito_percent"))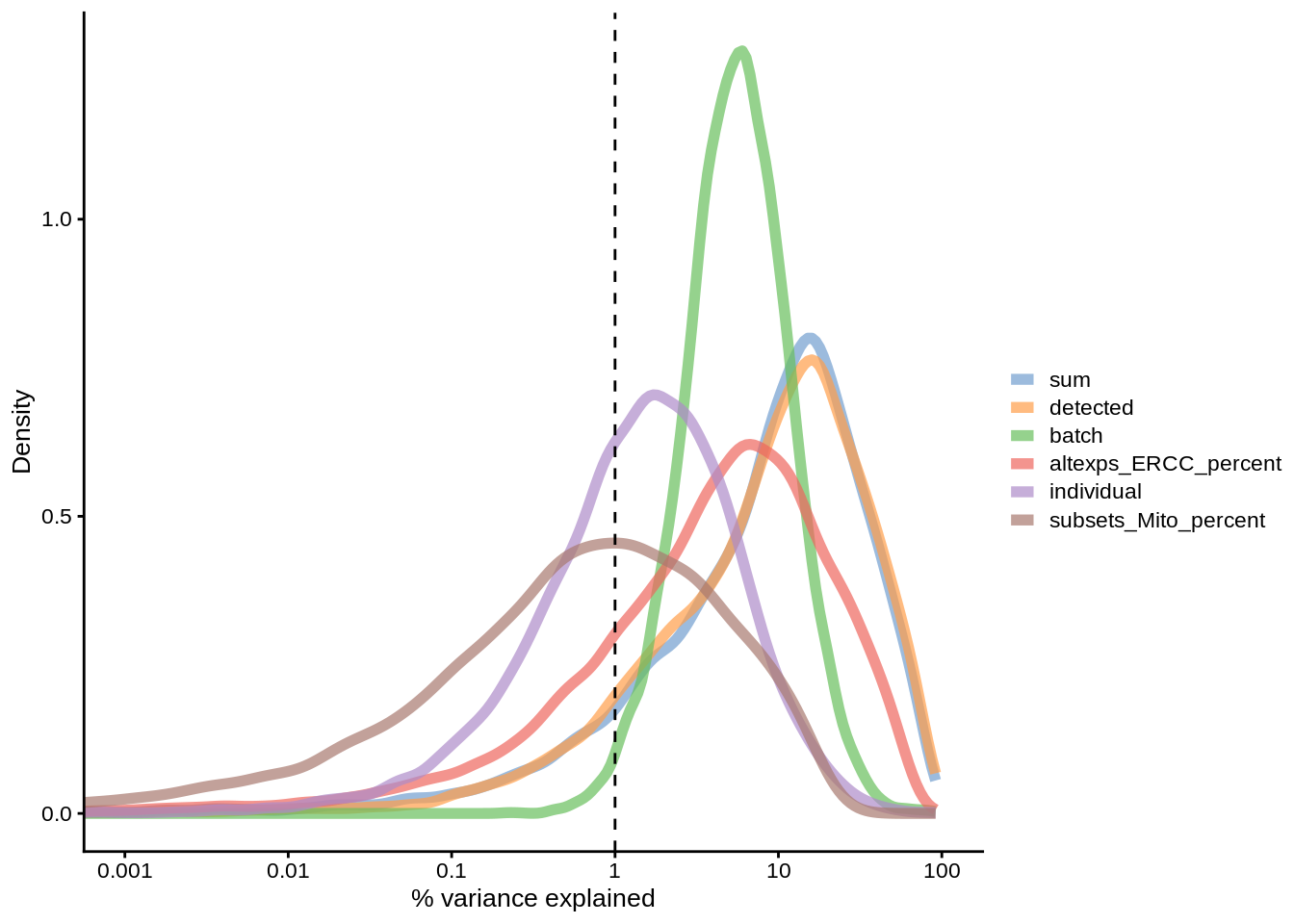
Figure 6.12: Explanatory variables
This analysis indicates that the number of detected genes (again) and also the sequencing depth (number of counts) have substantial explanatory power for many genes, so these variables are good candidates for conditioning out in a normalisation step, or including in downstream statistical models. Expression of ERCCs also appears to be an important explanatory variable and one notable feature of the above plot is that batch explains more than individual. What does that tell us about the technical and biological variability of the data?
6.3.4 Other Confounders
In addition to correcting for batch, there are other factors that one may want to compensate for. As with batch correction, these adjustments require extrinsic information. One popular method is scLVM which allows you to identify and subtract the effect from processes such as cell-cycle or apoptosis.
In addition, protocols may differ in terms of their coverage of each transcript, their bias based on the average content of A/T nucleotides, or their ability to capture short transcripts. Ideally, we would like to compensate for all of these differences and biases.
6.3.5 Exercise
Perform the same analysis with read counts of the Blischak data. Use tung/reads.rds file to load the reads SCESet object. Once you have finished please compare your results to ours (next chapter).
6.3.6 sessionInfo()
View session info
## R version 4.2.1 (2022-06-23)
## Platform: x86_64-pc-linux-gnu (64-bit)
## Running under: Ubuntu 20.04.2 LTS
##
## Matrix products: default
## BLAS: /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.9.0
## LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.9.0
##
## locale:
## [1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
## [3] LC_TIME=en_US.UTF-8 LC_COLLATE=en_US.UTF-8
## [5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
## [7] LC_PAPER=en_US.UTF-8 LC_NAME=C
## [9] LC_ADDRESS=C LC_TELEPHONE=C
## [11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
##
## attached base packages:
## [1] stats4 stats graphics grDevices utils datasets methods
## [8] base
##
## other attached packages:
## [1] scales_1.2.0 EnsDb.Hsapiens.v86_2.99.0
## [3] ensembldb_2.20.2 AnnotationFilter_1.20.0
## [5] GenomicFeatures_1.48.3 org.Hs.eg.db_3.15.0
## [7] AnnotationDbi_1.58.0 scater_1.24.0
## [9] ggplot2_3.3.6 scuttle_1.6.2
## [11] SingleCellExperiment_1.18.0 SummarizedExperiment_1.26.1
## [13] Biobase_2.56.0 GenomicRanges_1.48.0
## [15] GenomeInfoDb_1.32.2 IRanges_2.30.0
## [17] S4Vectors_0.34.0 BiocGenerics_0.42.0
## [19] MatrixGenerics_1.8.1 matrixStats_0.62.0
## [21] knitr_1.39
##
## loaded via a namespace (and not attached):
## [1] Rtsne_0.16 ggbeeswarm_0.6.0
## [3] colorspace_2.0-3 rjson_0.2.21
## [5] ellipsis_0.3.2 XVector_0.36.0
## [7] BiocNeighbors_1.14.0 farver_2.1.1
## [9] ggrepel_0.9.1 bit64_4.0.5
## [11] fansi_1.0.3 xml2_1.3.3
## [13] codetools_0.2-18 sparseMatrixStats_1.8.0
## [15] cachem_1.0.6 jsonlite_1.8.0
## [17] Rsamtools_2.12.0 dbplyr_2.2.1
## [19] png_0.1-7 compiler_4.2.1
## [21] httr_1.4.3 assertthat_0.2.1
## [23] Matrix_1.4-1 fastmap_1.1.0
## [25] lazyeval_0.2.2 cli_3.3.0
## [27] BiocSingular_1.12.0 htmltools_0.5.2
## [29] prettyunits_1.1.1 tools_4.2.1
## [31] rsvd_1.0.5 gtable_0.3.0
## [33] glue_1.6.2 GenomeInfoDbData_1.2.8
## [35] dplyr_1.0.9 rappdirs_0.3.3
## [37] Rcpp_1.0.9 jquerylib_0.1.4
## [39] vctrs_0.4.1 Biostrings_2.64.0
## [41] rtracklayer_1.56.1 DelayedMatrixStats_1.18.0
## [43] xfun_0.31 stringr_1.4.0
## [45] beachmat_2.12.0 lifecycle_1.0.1
## [47] irlba_2.3.5 restfulr_0.0.15
## [49] XML_3.99-0.10 zlibbioc_1.42.0
## [51] ProtGenerics_1.28.0 hms_1.1.1
## [53] parallel_4.2.1 yaml_2.3.5
## [55] curl_4.3.2 memoise_2.0.1
## [57] gridExtra_2.3 sass_0.4.1
## [59] biomaRt_2.52.0 stringi_1.7.8
## [61] RSQLite_2.2.14 highr_0.9
## [63] BiocIO_1.6.0 ScaledMatrix_1.4.0
## [65] filelock_1.0.2 BiocParallel_1.30.3
## [67] rlang_1.0.4 pkgconfig_2.0.3
## [69] bitops_1.0-7 evaluate_0.15
## [71] lattice_0.20-45 purrr_0.3.4
## [73] labeling_0.4.2 GenomicAlignments_1.32.0
## [75] cowplot_1.1.1 bit_4.0.4
## [77] tidyselect_1.1.2 magrittr_2.0.3
## [79] bookdown_0.27 R6_2.5.1
## [81] generics_0.1.3 DelayedArray_0.22.0
## [83] DBI_1.1.3 pillar_1.7.0
## [85] withr_2.5.0 KEGGREST_1.36.3
## [87] RCurl_1.98-1.7 tibble_3.1.7
## [89] crayon_1.5.1 utf8_1.2.2
## [91] BiocFileCache_2.4.0 rmarkdown_2.14
## [93] viridis_0.6.2 progress_1.2.2
## [95] grid_4.2.1 blob_1.2.3
## [97] digest_0.6.29 munsell_0.5.0
## [99] beeswarm_0.4.0 viridisLite_0.4.0
## [101] vipor_0.4.5 bslib_0.3.16.4 Normalization Theory
6.4.1 Introduction
In the previous chapter we identified important confounding factors and explanatory variables. scater allows one to account for these variables in subsequent statistical models or to condition them out using normaliseExprs(), if so desired. This can be done by providing a design matrix to normaliseExprs(). We are not covering this topic here, but you can try to do it yourself as an exercise.
Instead we will explore how simple size-factor normalisations correcting for library size can remove the effects of some of the confounders and explanatory variables.
6.4.2 Library Size
Library sizes vary because scRNA-seq data is often sequenced on highly multiplexed platforms the total reads which are derived from each cell may differ substantially. Some quantification methods (eg. Cufflinks, RSEM) incorporated library size when determining gene expression estimates thus do not require this normalization.
However, if another quantification method was used then library size must be corrected for by multiplying or dividing each column of the expression matrix by a “normalization factor” which is an estimate of the library size relative to the other cells. Many methods to correct for library size have been developped for bulk RNA-seq and can be equally applied to scRNA-seq (eg. UQ, SF, CPM, RPKM, FPKM, TPM).
6.4.3 Normalisations
6.4.3.1 CPM
The simplest way to normalize this data is to convert it to counts per million (CPM) by dividing each column by its total then multiplying by 1,000,000. Note that spike-ins should be excluded from the calculation of total expression in order to correct for total cell RNA content, therefore we will only use endogenous genes. Example of a CPM function in R:
One potential drawback of CPM is if your sample contains genes that are both very highly expressed and differentially expressed across the cells. In this case, the total molecules in the cell may depend of whether such genes are on/off in the cell and normalizing by total molecules may hide the differential expression of those genes and/or falsely create differential expression for the remaining genes.
Note RPKM, FPKM and TPM are variants on CPM which further adjust counts by the length of the respective gene/transcript.
To deal with this potentiality several other measures were devised.
6.4.3.2 Relative Log Expression (RLE)
The size factor (SF) was proposed and popularized by DESeq (Anders and Huber 2010). First the geometric mean of each gene across all cells is calculated. The size factor for each cell is the median across genes of the ratio of the expression to the gene’s geometric mean. A drawback to this method is that since it uses the geometric mean only genes with non-zero expression values across all cells can be used in its calculation, making it unadvisable for large low-depth scRNA-seq experiments. edgeR & scater call this method RLE for “relative log expression.” Example of a SF function in R:
6.4.3.3 Upper Quartile (UQ) Normalization
The upperquartile (UQ) was proposed by (Bullard et al. 2010). Here each column is divided by the 75% quantile of the counts for each library. Often the calculated quantile is scaled by the median across cells to keep the absolute level of expression relatively consistent. A drawback to this method is that for low-depth scRNA-seq experiments the large number of undetected genes may result in the 75% quantile being zero (or close to it). This limitation can be overcome by generalizing the idea and using a higher quantile (eg. the 99% quantile is the default in scater) or by excluding zeros prior to calculating the 75% quantile. Example of a UQ function in R:
6.4.3.4 Trimmed Mean of M-values (TMM)
Another method is called TMM is the weighted trimmed mean of M-values (to the reference) proposed by (Robinson and Oshlack 2010). The M-values in question are the gene-wise log2 fold changes between individual cells. One cell is used as the reference then the M-values for each other cell is calculated compared to this reference. These values are then trimmed by removing the top and bottom ~30%, and the average of the remaining values is calculated by weighting them to account for the effect of the log scale on variance. Each non-reference cell is multiplied by the calculated factor. Two potential issues with this method are insufficient non-zero genes left after trimming, and the assumption that most genes are not differentially expressed.
6.4.3.5 scran
scran package implements a variant on CPM specialized for single-cell data (L. Lun, Bach, and Marioni 2016). Briefly, this method deals with the problem of vary large numbers of zero values per cell by pooling cells together calculating a normalization factor (similar to CPM) for the sum of each pool. Since each cell is found in many different pools, cell-specific factors can be deconvoluted from the collection of pool-specific factors using linear algebraic methods.
6.4.3.6 Downsampling
Finally, a simple way to correct for library size is to downsample the expression matrix so that each cell has approximately the same total number of molecules. The benefit of this method is that zero values will be introduced by the downsampling, thus eliminating any biases due to differing numbers of detected genes. However, the major drawback is that the process is not-deterministic, so each time the downsampling is run the resulting expression matrix is slightly different. Thus, often analyses must be run on multiple downsamplings to ensure results are robust. Example of a downsampling function in R:
6.4.4 Effectiveness
To compare the efficiency of different normalization methods we will use visual inspection of PCA plots and calculation of cell-wise relative log expression via scater’s plotRLE() function. Namely, cells with many (few) reads have higher (lower) than median expression for most genes resulting in a positive (negative) RLE across the cell, whereas normalized cells have an RLE close to zero. Example of a RLE function in R:
Note The RLE, TMM, and UQ size-factor methods were developed for bulk RNA-seq data and, depending on the experimental context, may not be appropriate for single-cell RNA-seq data, as their underlying assumptions may be problematically violated.
Note scater acts as a wrapper for the calcNormFactors function from edgeR which implements several library size normalization methods making it easy to apply any of these methods to our data.
Note edgeR makes extra adjustments to some of the normalization methods which may result in somewhat different results than if the original methods are followed exactly, e.g. edgeR’s and scater’s “RLE” method which is based on the “size factor” used by DESeq may give different results to the estimateSizeFactorsForMatrix method in the DESeq/DESeq2 packages. In addition, some versions of edgeR will not calculate the normalization factors correctly unless lib.size is set at 1 for all cells.
Note For CPM normalisation we use scater’s calculateCPM() function. For RLE, UQ and TMM we used to use scater’s normaliseExprs() function (it is deprecated now and therefore we removed the corresponding subchapters). For scran we use scran package to calculate size factors (it also operates on SingleCellExperiment class) and scater’s normalize() to normalise the data. All these normalization functions save the results to the logcounts slot of the SCE object. For downsampling we use our own functions shown above.
6.5 Normalization Practice
We will continue to work with the tung data that was used in the previous chapter.
library(scRNA.seq.funcs)
library(scater)
library(scran)
set.seed(1234567)
umi <- readRDS("data/tung/umi.rds")
umi.qc <- umi[! rowData(umi)$discard, ! colData(umi)$discard]6.5.1 PCA on logcounts_raw data
Log transformation makes the data group intuitively (e.g., by individual). However, there is clear dependency on the sequencing depth.
umi.qc <- runPCA(umi.qc, exprs_values = "logcounts_raw")
plotPCA(umi.qc, colour_by = "batch", size_by = "detected", shape_by = "individual")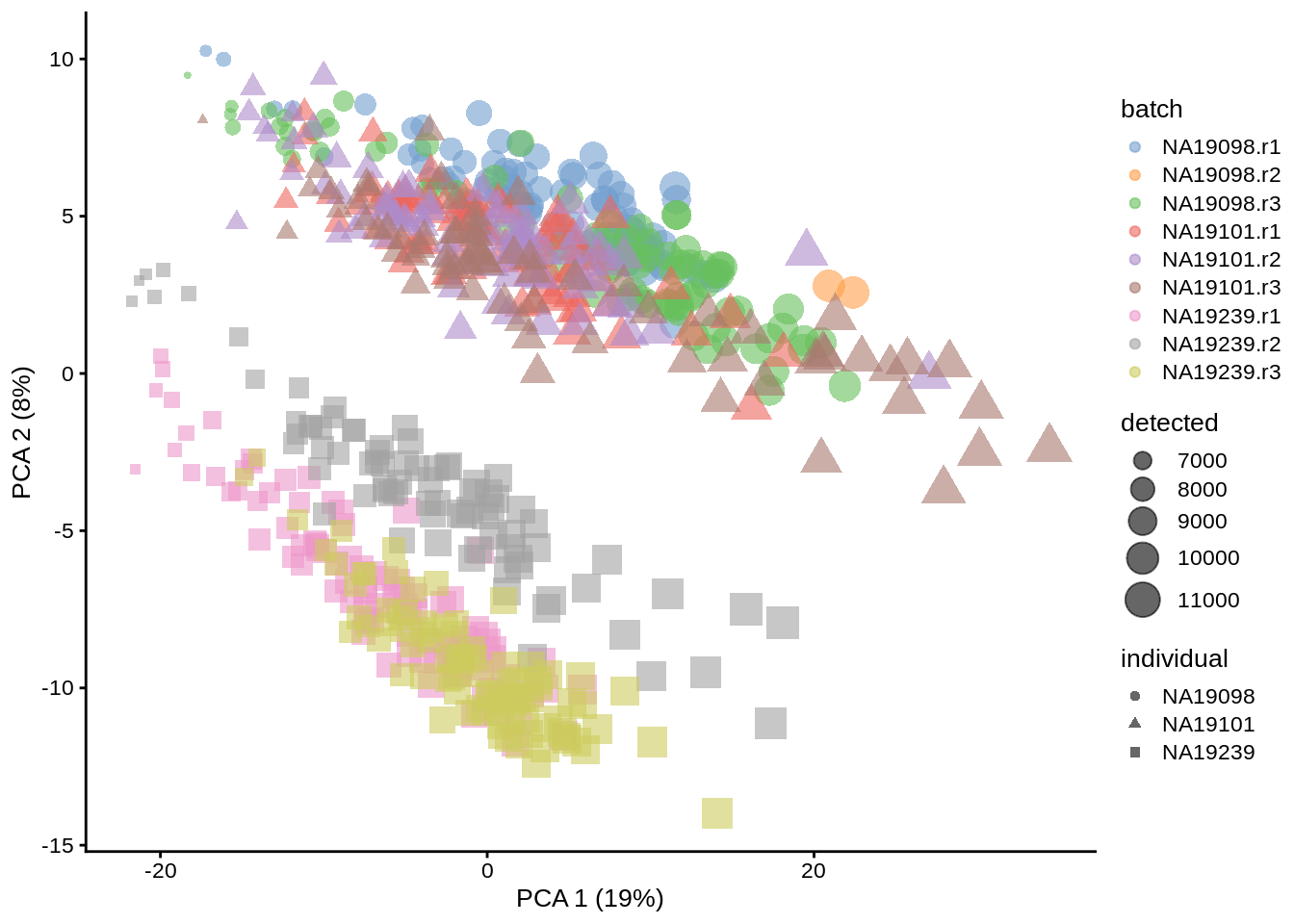
Figure 6.13: PCA plot of the Tung data (logcounts raw)
6.5.2 PCA on CPM-normalized data
For future exercises, note that assay named logcounts is the default for most plotting and dimensionality reduction functions. We shall populate it with various normalizations and compare the results. The logcounts assay and PCA reducedDim objects are replaced every time we re-do normalization or runPCA.
logcounts(umi.qc) <- log2(calculateCPM(umi.qc) + 1)
umi.qc <- runPCA(umi.qc)
plotPCA(umi.qc, colour_by = "batch", size_by = "detected", shape_by = "individual")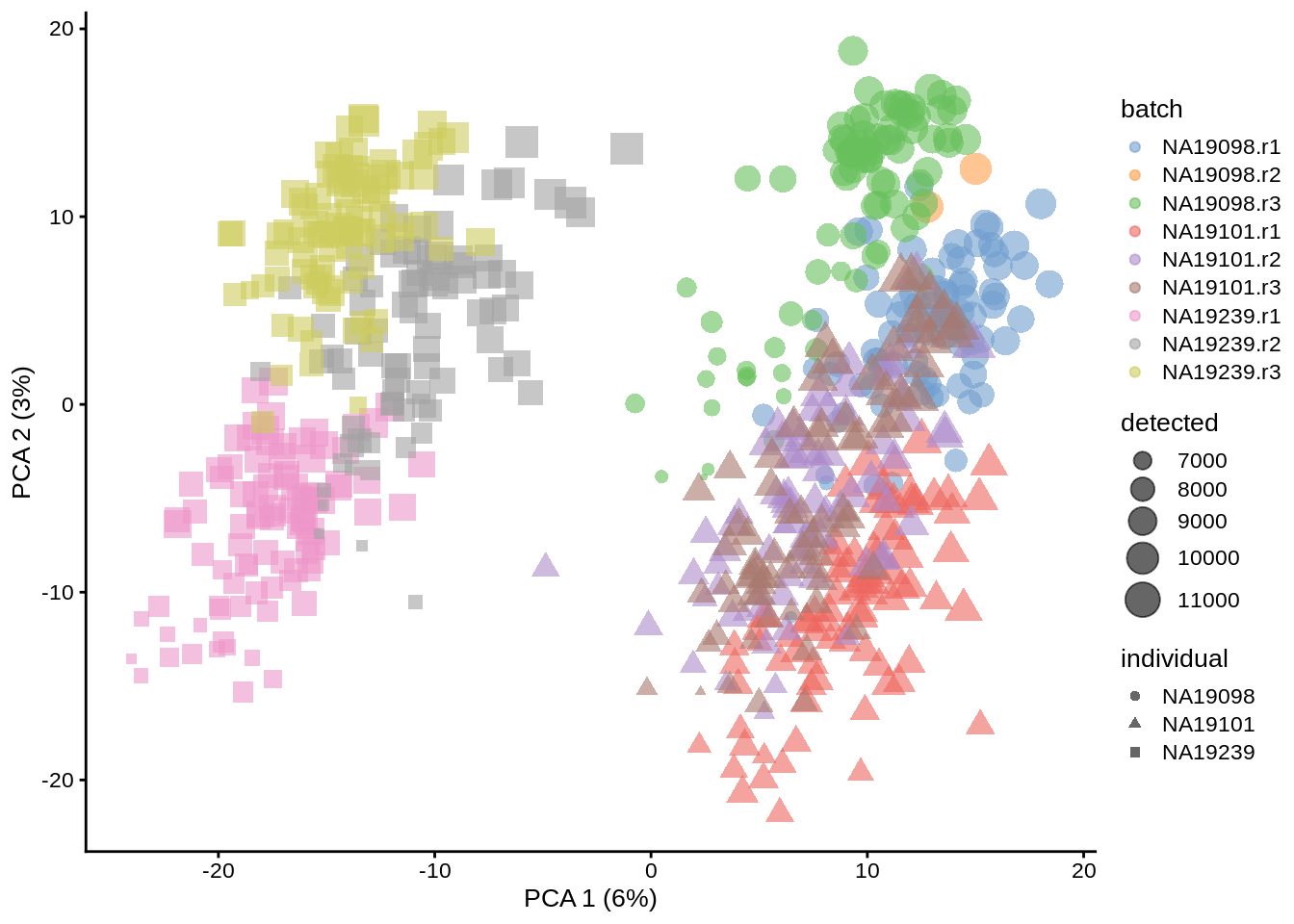
Figure 6.14: PCA plot of the tung data after CPM normalisation
A relative log expression (RLE) plots can be very useful assessing whether normalization procedure was successful.
plotRLE(umi.qc, exprs_values = "logcounts_raw",colour_by = "batch") + ggtitle("RLE plot for logcounts_raw")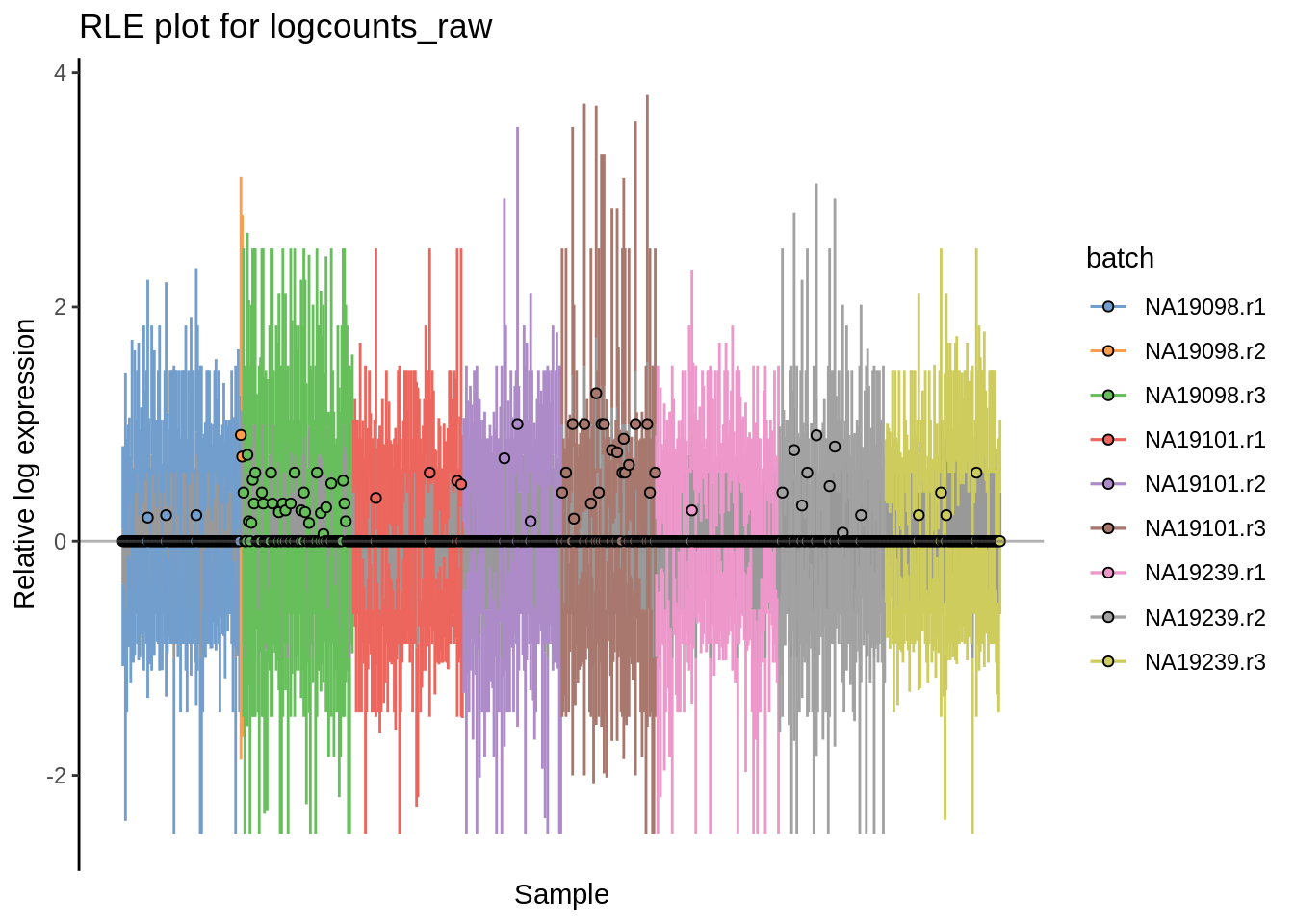
Figure 6.15: Cell-wise RLE for logcounts-raw and log2-transformed CPM counts
plotRLE(umi.qc, exprs_values = "logcounts",colour_by = "batch") + ggtitle("RLE plot for log2(CPM) counts")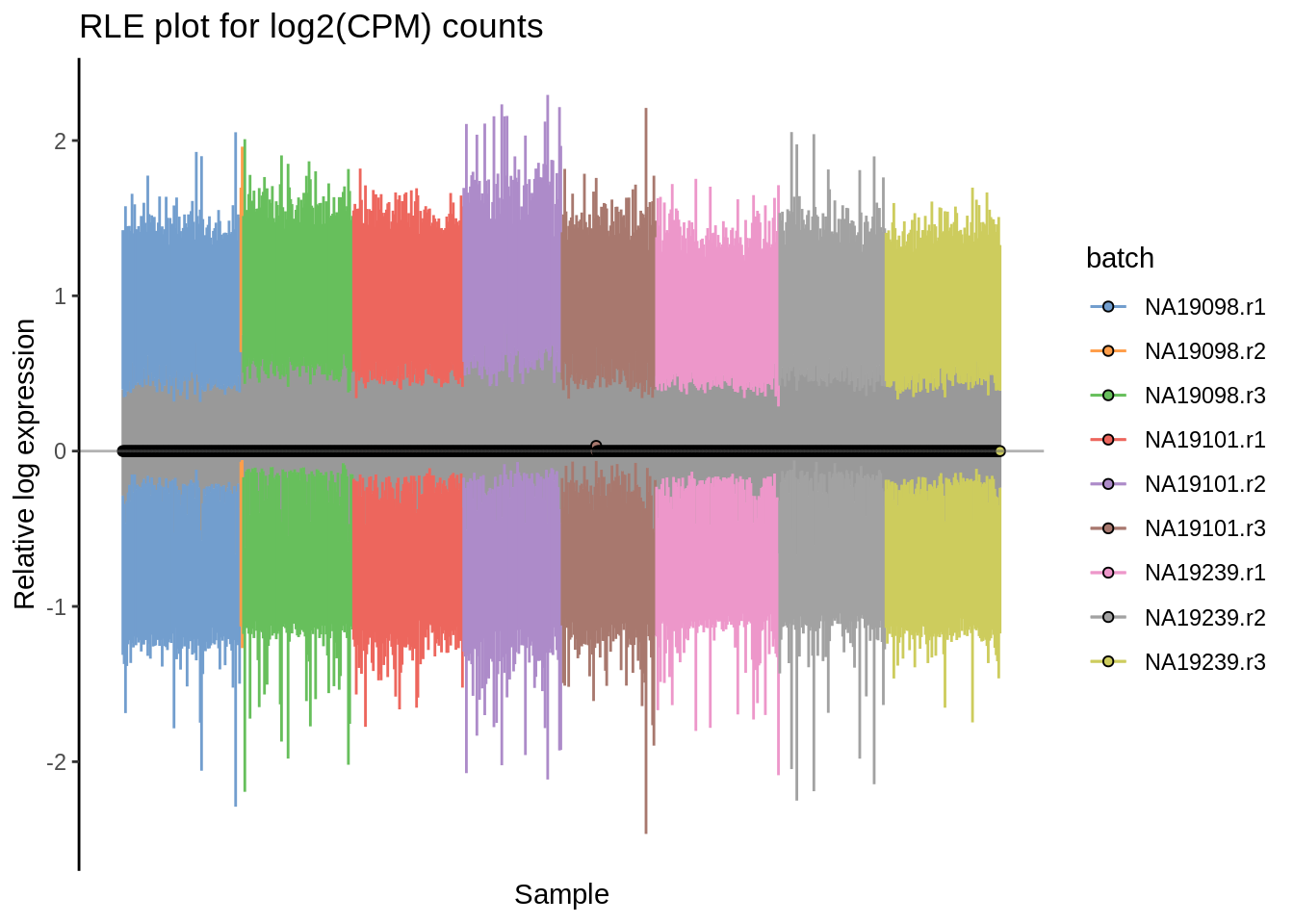
Figure 6.16: Cell-wise RLE for logcounts-raw and log2-transformed CPM counts
6.5.3 PCA on scran-normalized Data
CPM-based and other similar library-wise scaling approaches assume that all cells contain similar amounts of RNA, and hence should produce similar UMI counts. This is not always true. The following method, available in scran and several other bioconductoR packages, uses clustering in order to make normalization. This is sometimes referred to as normalization by deconvolution. First, let’s do a quick-and-dirty clustering. These clusters look conspicuously like our batches!
qclust <- quickCluster(umi.qc, min.size = 30)
table(qclust)## qclust
## 1 2 3 4 5 6 7 8
## 86 77 81 94 90 88 66 88Next, let’s compute the size factors using the clustering. The first function adds a column to colData named sizeFactor. These values are then used by logNormCounts.
umi.qc <- computeSumFactors(umi.qc, clusters = qclust)## Warning in .guessMinMean(x, min.mean = min.mean, BPPARAM = BPPARAM): assuming
## UMI data when setting 'min.mean'umi.qc <- logNormCounts(umi.qc)We now can see much higher resolution of individual and replicate-based batches.
umi.qc <- runPCA(umi.qc)
plotPCA(umi.qc, colour_by = "batch",size_by = "detected", shape_by = "individual")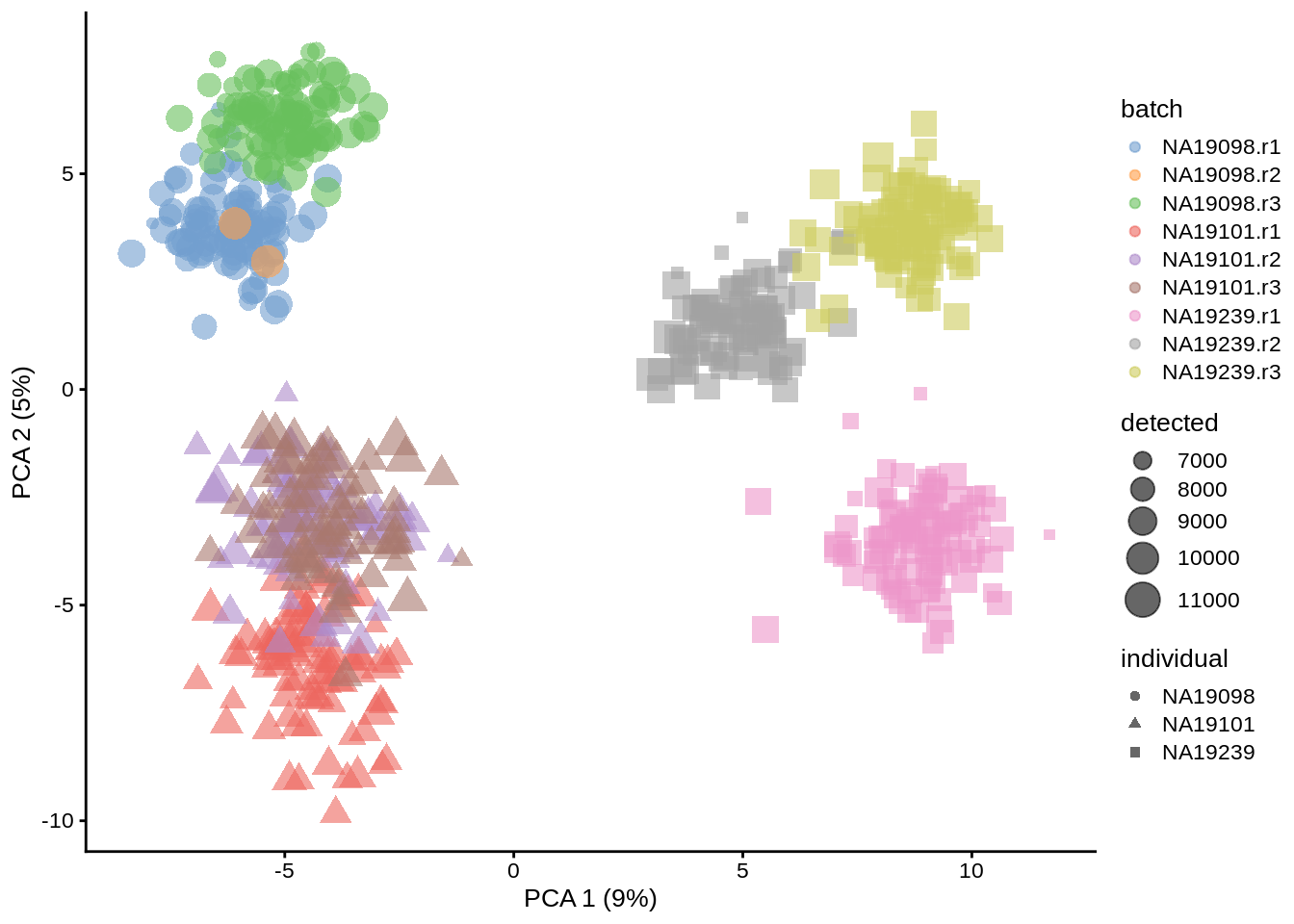
Figure 6.17: PCA plot of the tung data after deconvolution-based (scran) normalisation
RLE plots also displays a nicely regularized plot.
plotRLE(umi.qc, exprs_values = "logcounts",colour_by = "batch")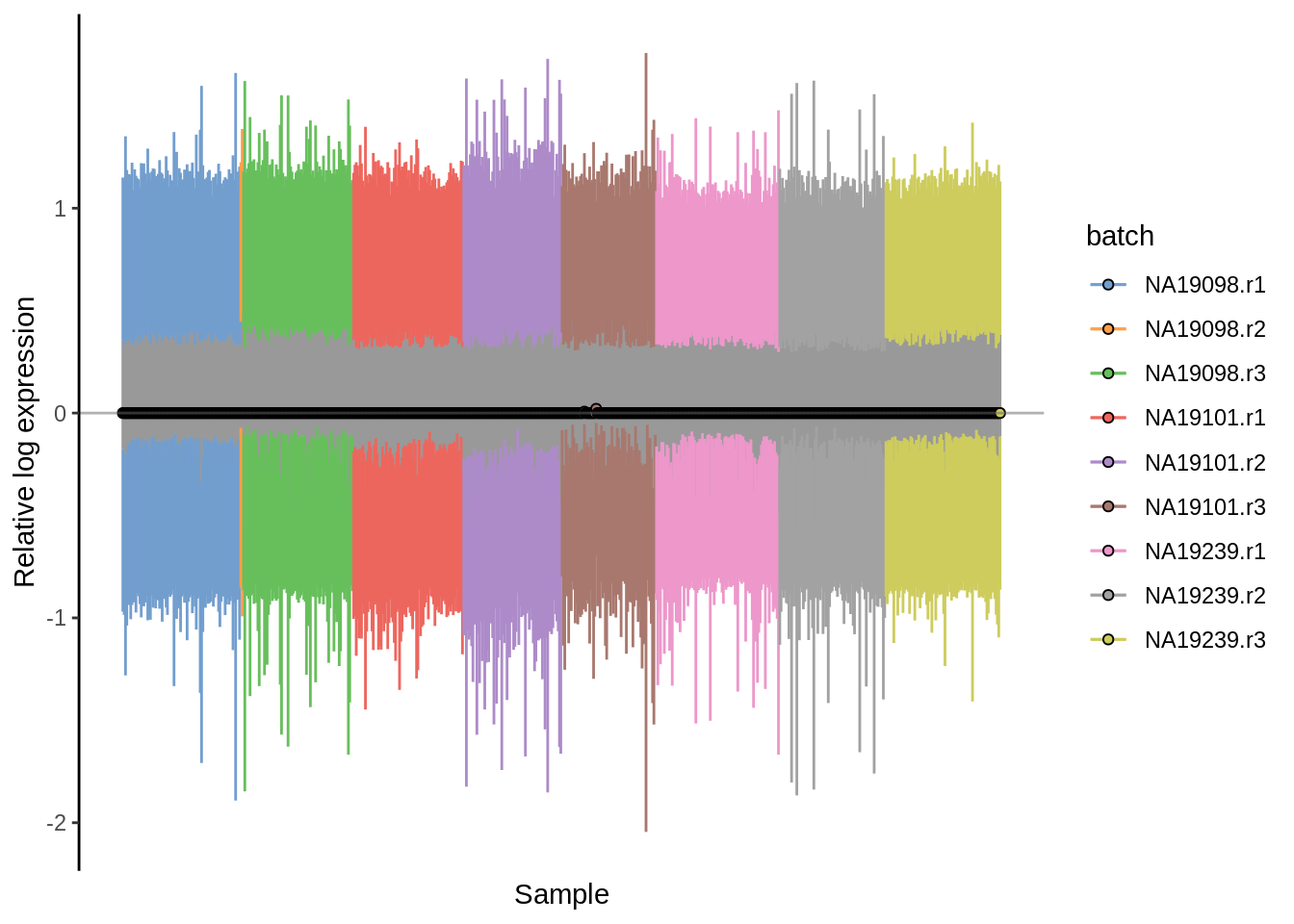
Figure 6.18: Cell-wise RLE of the tung data
Sometimes scran produces negative or zero size factors. These will completely distort the normalized expression matrix. We can check the size factors scran has computed like so:
summary(sizeFactors(umi.qc))## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.3821 0.7710 0.9524 1.0000 1.1490 3.2732For this dataset all the size factors are well-behaved; we will use this normalization for further analysis. If you find scran has calculated negative size factors try increasing the cluster and pool sizes until they are all positive.
6.5.4 PCA with Downsampled Data
logcounts(umi.qc) <- log2(Down_Sample_Matrix(counts(umi.qc)) + 1)
umi.qc <- runPCA(umi.qc)
plotPCA(umi.qc,colour_by = "batch",size_by = "detected", shape_by = "individual")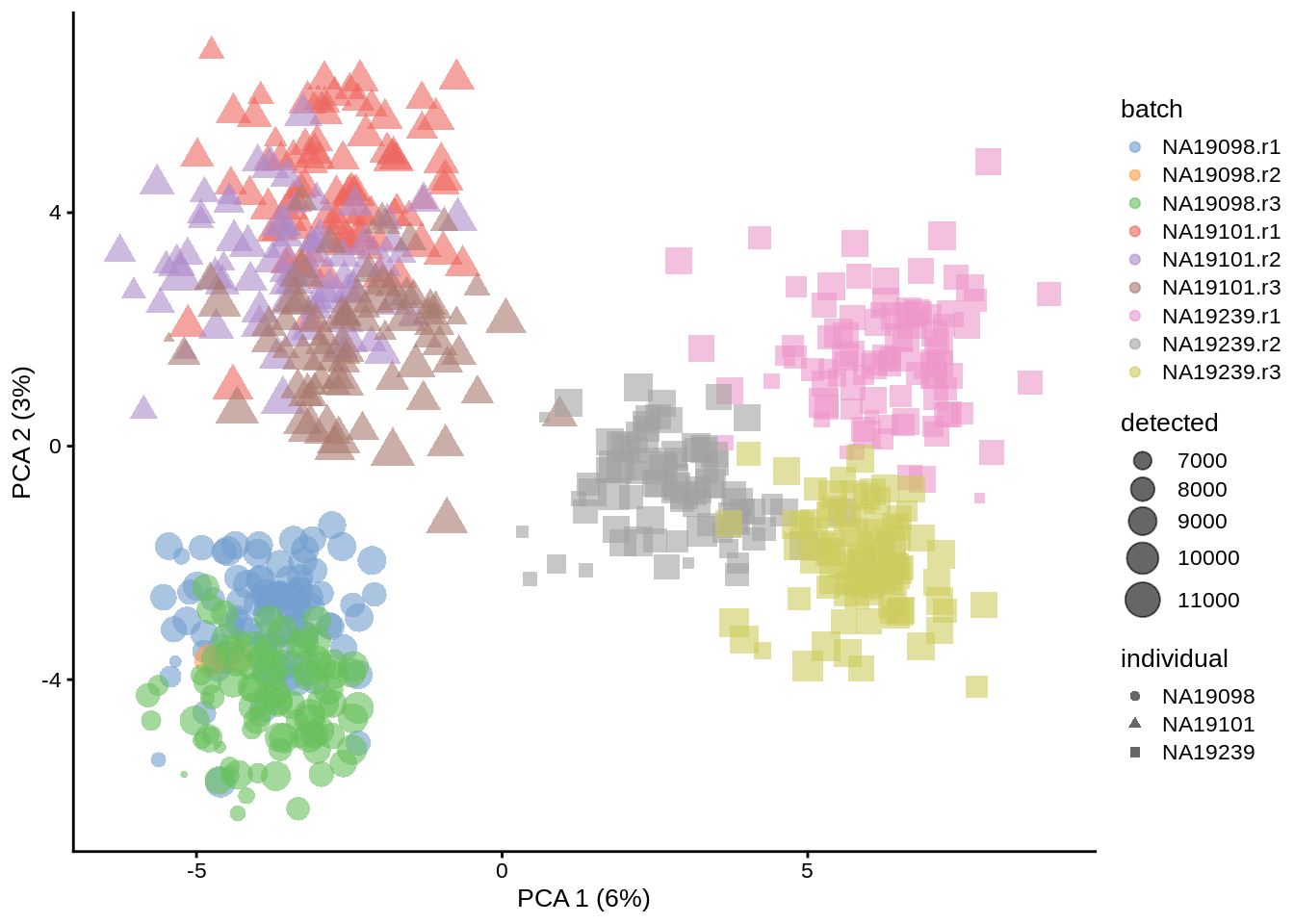
Figure 6.19: PCA plot of the tung data after downsampling
plotRLE(umi.qc, exprs_values = "logcounts",colour_by = "batch")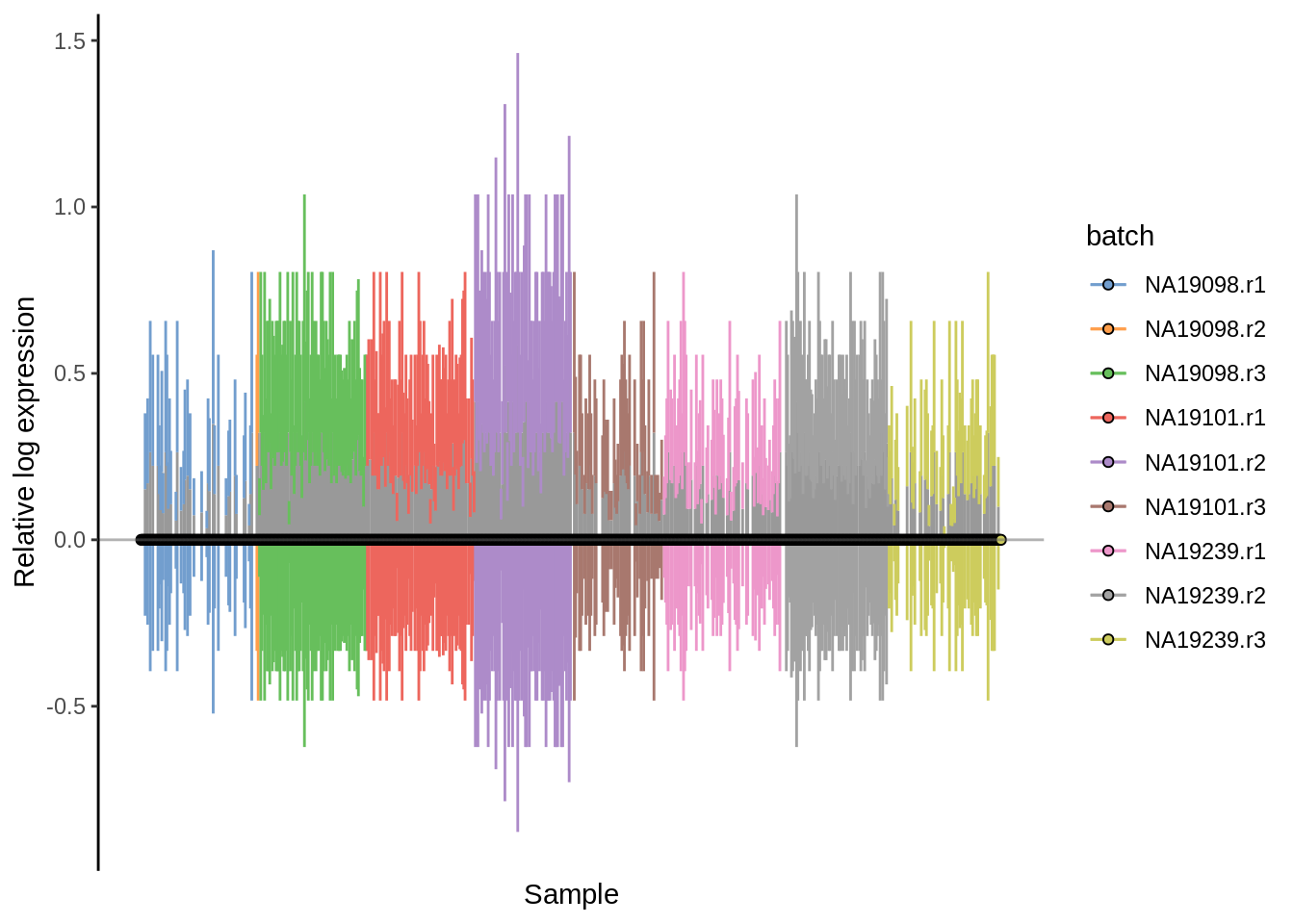
Figure 6.20: Cell-wise RLE of the tung data (normalization by downsampling)
6.5.5 sessionInfo()
View session info
## R version 4.2.1 (2022-06-23)
## Platform: x86_64-pc-linux-gnu (64-bit)
## Running under: Ubuntu 20.04.2 LTS
##
## Matrix products: default
## BLAS: /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.9.0
## LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.9.0
##
## locale:
## [1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
## [3] LC_TIME=en_US.UTF-8 LC_COLLATE=en_US.UTF-8
## [5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
## [7] LC_PAPER=en_US.UTF-8 LC_NAME=C
## [9] LC_ADDRESS=C LC_TELEPHONE=C
## [11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
##
## attached base packages:
## [1] stats4 stats graphics grDevices utils datasets methods
## [8] base
##
## other attached packages:
## [1] scran_1.24.0 scater_1.24.0
## [3] ggplot2_3.3.6 scuttle_1.6.2
## [5] SingleCellExperiment_1.18.0 SummarizedExperiment_1.26.1
## [7] Biobase_2.56.0 GenomicRanges_1.48.0
## [9] GenomeInfoDb_1.32.2 IRanges_2.30.0
## [11] S4Vectors_0.34.0 BiocGenerics_0.42.0
## [13] MatrixGenerics_1.8.1 matrixStats_0.62.0
## [15] knitr_1.39 scRNA.seq.funcs_0.1.0
##
## loaded via a namespace (and not attached):
## [1] bitops_1.0-7 tools_4.2.1
## [3] bslib_0.3.1 utf8_1.2.2
## [5] R6_2.5.1 irlba_2.3.5
## [7] hypergeo_1.2-13 vipor_0.4.5
## [9] DBI_1.1.3 colorspace_2.0-3
## [11] withr_2.5.0 tidyselect_1.1.2
## [13] gridExtra_2.3 moments_0.14.1
## [15] compiler_4.2.1 orthopolynom_1.0-6
## [17] cli_3.3.0 BiocNeighbors_1.14.0
## [19] DelayedArray_0.22.0 labeling_0.4.2
## [21] bookdown_0.27 sass_0.4.1
## [23] scales_1.2.0 stringr_1.4.0
## [25] digest_0.6.29 rmarkdown_2.14
## [27] XVector_0.36.0 pkgconfig_2.0.3
## [29] htmltools_0.5.2 sparseMatrixStats_1.8.0
## [31] highr_0.9 limma_3.52.2
## [33] fastmap_1.1.0 rlang_1.0.4
## [35] DelayedMatrixStats_1.18.0 farver_2.1.1
## [37] jquerylib_0.1.4 generics_0.1.3
## [39] jsonlite_1.8.0 BiocParallel_1.30.3
## [41] dplyr_1.0.9 RCurl_1.98-1.7
## [43] magrittr_2.0.3 BiocSingular_1.12.0
## [45] polynom_1.4-1 GenomeInfoDbData_1.2.8
## [47] Matrix_1.4-1 Rcpp_1.0.9
## [49] ggbeeswarm_0.6.0 munsell_0.5.0
## [51] fansi_1.0.3 viridis_0.6.2
## [53] lifecycle_1.0.1 edgeR_3.38.1
## [55] stringi_1.7.8 yaml_2.3.5
## [57] MASS_7.3-58 zlibbioc_1.42.0
## [59] Rtsne_0.16 grid_4.2.1
## [61] dqrng_0.3.0 parallel_4.2.1
## [63] ggrepel_0.9.1 crayon_1.5.1
## [65] contfrac_1.1-12 lattice_0.20-45
## [67] cowplot_1.1.1 beachmat_2.12.0
## [69] locfit_1.5-9.6 metapod_1.4.0
## [71] pillar_1.7.0 igraph_1.3.2
## [73] codetools_0.2-18 ScaledMatrix_1.4.0
## [75] glue_1.6.2 evaluate_0.15
## [77] deSolve_1.32 vctrs_0.4.1
## [79] gtable_0.3.0 purrr_0.3.4
## [81] assertthat_0.2.1 xfun_0.31
## [83] rsvd_1.0.5 viridisLite_0.4.0
## [85] tibble_3.1.7 elliptic_1.4-0
## [87] beeswarm_0.4.0 cluster_2.1.3
## [89] bluster_1.6.0 statmod_1.4.36
## [91] ellipsis_0.3.26.6 Dealing with Confounders
6.6.1 Introduction
In the previous chapter we normalized for library size, effectively removing it as a confounder. Now we will consider removing other less well-defined confounders from our data. Technical confounders (aka batch effects) can arise from difference in reagents, isolation methods, the lab/experimenter who performed the experiment, even which day or time of the day the experiment was performed. Accounting for technical confounders, and batch effects particularly, is a large topic that also involves principles of experimental design. Here we address approaches that can be taken to account for confounders when the experimental design is appropriate.
Fundamentally, accounting for technical confounders involves identifying and, ideally, removing sources of variation in the expression data that are not related to (i.e. are confounding) the biological signal of interest. Various approaches exist, some of which use spike-in or housekeeping genes, and some of which use endogenous genes.
The use of spike-ins as control genes is appealing, since the same amount of ERCC (or other) spike-in was added to each cell in our experiment. In principle, all the variablity we observe for these genes is due to technical noise; whereas endogenous genes are affected by both technical noise and biological variability. Technical noise can be removed by fitting a model to the spike-ins and “substracting” this from the endogenous genes. There are several methods available based on this premise (eg. BASiCS, scLVM, RUVg); each using different noise models and different fitting procedures. Alternatively, one can identify genes which exhibit significant variation beyond technical noise (eg. Distance to median, Highly variable genes). However, there are issues with the use of spike-ins for normalisation (particularly ERCCs, derived from bacterial sequences), including that their variability can, for various reasons, actually be higher than that of endogenous genes.
Given the issues with using spike-ins, better results can often be obtained by using endogenous genes instead. Where we have a large number of endogenous genes that, on average, do not vary systematically between cells and where we expect technical effects to affect a large number of genes (a very common and reasonable assumption), then such methods (for example, the RUVs method) can perform well.
There are two scenarios in scRNA-seq dataset integration. In the first scenario, cell composition is expected to be the same, and methods developed for bulk RNA-seq (e.g. ComBat) exhibit good performance. This is often true for biological replicates of the same experiment; this is also true for batches in tung dataset. In the second scenario, the overlap between the datasets is partial - e.g. if datasets represent healthy and diseased tissue, which differ in cell type composition substantially. In this case, mutual nearest neighbor (MNN)-based methods tend to perform much better. We will look at these
Here, we will perform batch correction using two methods - ComBat, based on empirical Bayesian framework, and fastMNN, which is a MNN-based method from the package batchelor.
6.6.2 Load and Normalize the Tung Dataset
library(scRNA.seq.funcs)
library(scater)
library(scran)
library(sva)
library(batchelor)
library(kBET)
set.seed(1234567)Let’s read in the pre-processed dataset and normalize it using logNormCounts from scran package. In umi.qc object, a new assay named logcounts will appear, in addition to the previously present counts and logcounts_raw:
umi <- readRDS("data/tung/umi.rds")
umi.qc <- umi[! rowData(umi)$discard, ! colData(umi)$discard]
qclust <- quickCluster(umi.qc, min.size = 30)
umi.qc <- computeSumFactors(umi.qc, clusters = qclust)## Warning in .guessMinMean(x, min.mean = min.mean, BPPARAM = BPPARAM): assuming
## UMI data when setting 'min.mean'umi.qc <- logNormCounts(umi.qc)6.6.3 Combat
If you have an experiment with a balanced design, ComBat can be used to eliminate batch effects while preserving biological effects by specifying the biological effects using the mod parameter. However the Tung data contains multiple experimental replicates rather than a balanced design so using mod1 to preserve biological variability will result in an error.
assay(umi.qc, "combat") <- ComBat(logcounts(umi.qc),batch = umi.qc$replicate)## Found 40 genes with uniform expression within a single batch (all zeros); these will not be adjusted for batch.## Found3batches## Adjusting for0covariate(s) or covariate level(s)## Standardizing Data across genes## Fitting L/S model and finding priors## Finding parametric adjustments## Adjusting the DataExercise 1
Perform ComBat correction accounting for total features as a co-variate. Store the corrected matrix in the combat_tf slot.
Answer
assay(umi.qc, "combat_tf") <- ComBat(logcounts(umi.qc),batch = umi.qc$detected)## Found 9416 genes with uniform expression within a single batch (all zeros); these will not be adjusted for batch.## Using the 'mean only' version of ComBat## Found609batches## Note: one batch has only one sample, setting mean.only=TRUE## Adjusting for0covariate(s) or covariate level(s)## Standardizing Data across genes## Fitting L/S model and finding priors## Finding parametric adjustments## Adjusting the Data6.6.4 mnnCorrect (batchelor)
MNN-based normalization is implemented as fastMNN function.
mnn_out <- fastMNN(umi.qc,batch = umi.qc$replicate)
assay(umi.qc, "mnn") <- assay(mnn_out,'reconstructed')6.6.5 Evaluation and Comparison of Batch-removal Approaches
A key question when considering the different methods for removing confounders is how to quantitatively determine which one is the most effective. The main reason why comparisons are challenging is because it is often difficult to know what corresponds to technical counfounders and what is interesting biological variability. Here, we consider three different metrics which are all reasonable based on our knowledge of the experimental design. Depending on the biological question that you wish to address, it is important to choose a metric that allows you to evaluate the confounders that are likely to be the biggest concern for the given situation.
6.6.5.1 Effectiveness 1
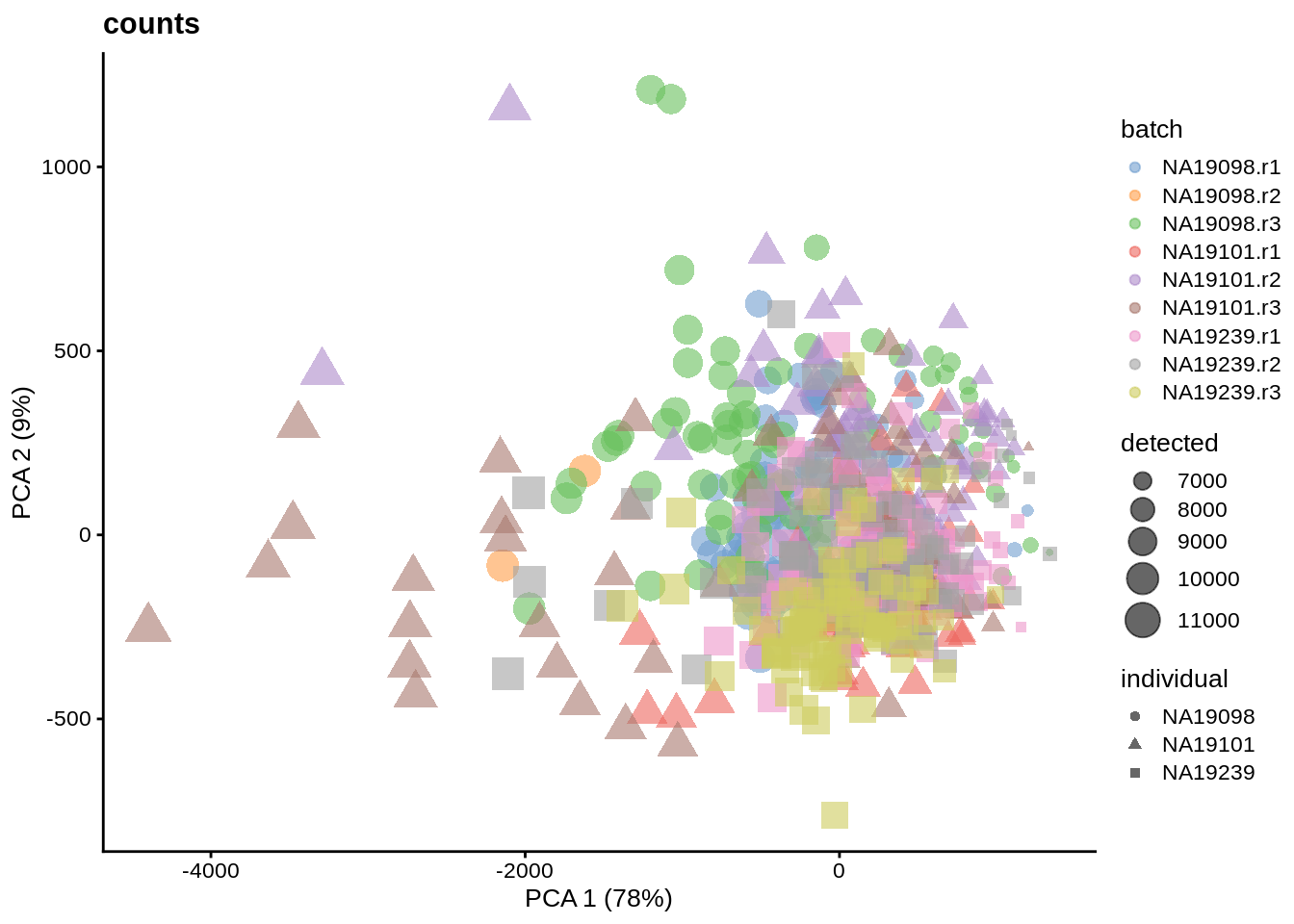
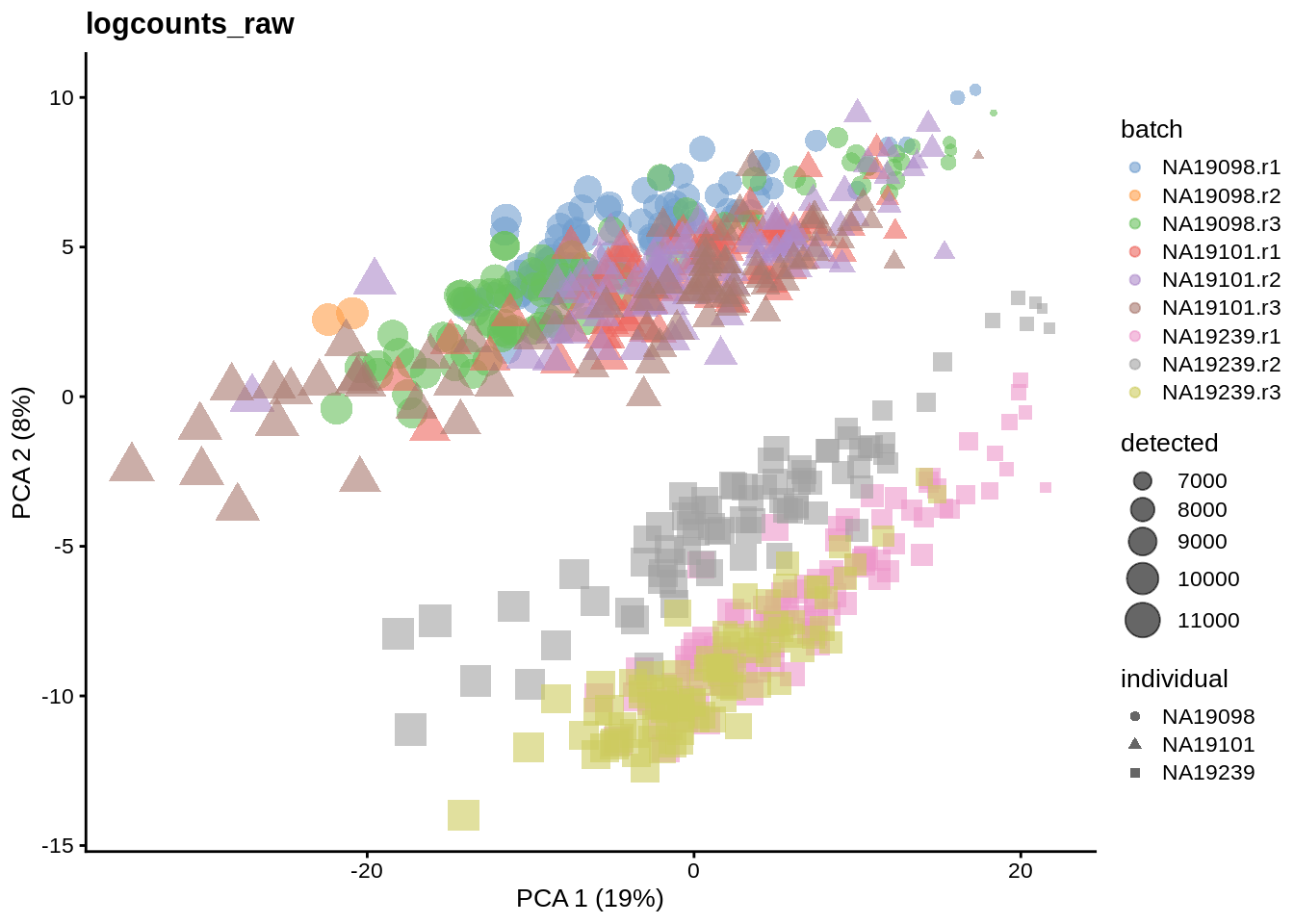
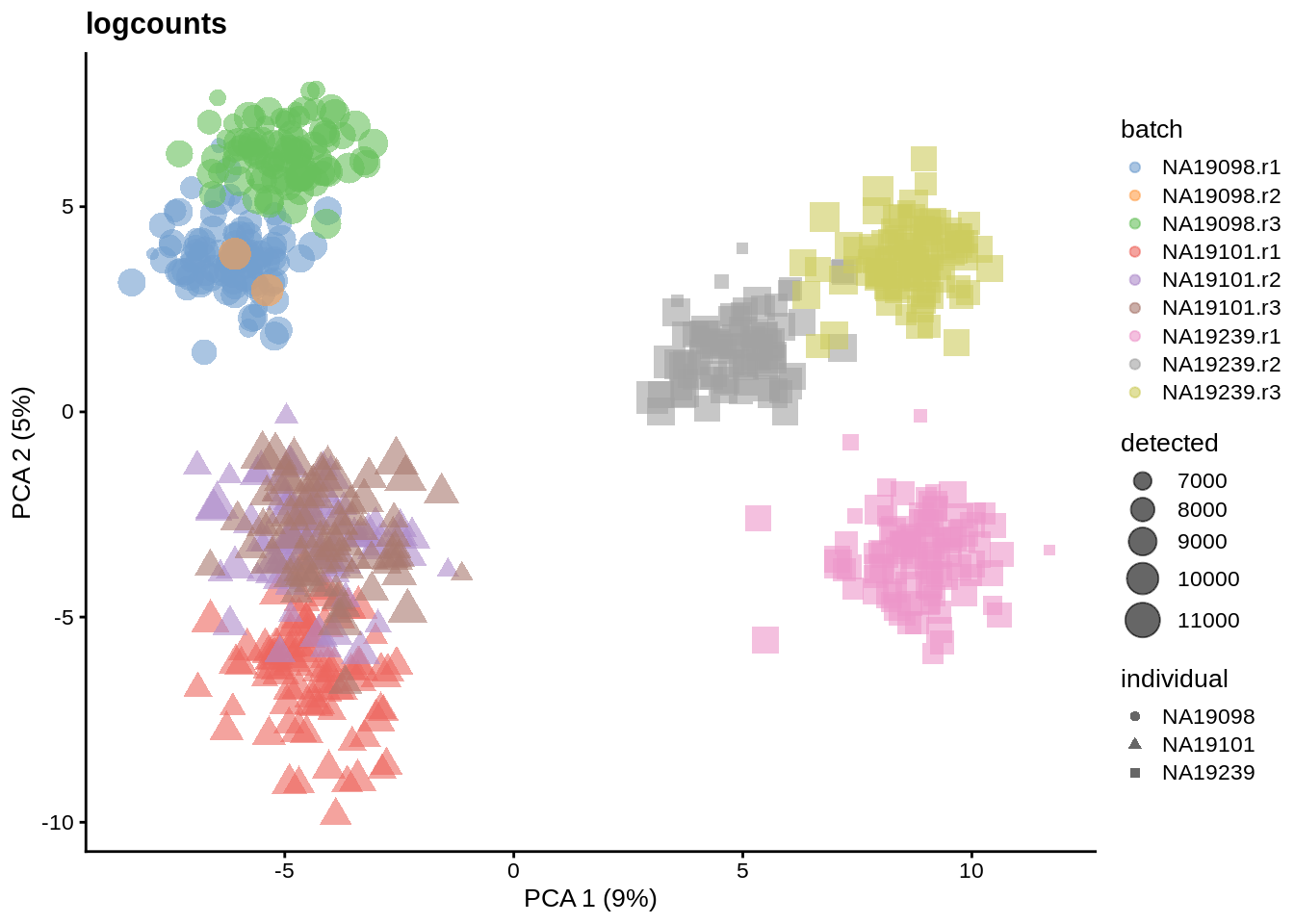
We evaluate the effectiveness of the normalization by inspecting the PCA plot where colour corresponds the technical replicates and shape corresponds to different biological samples (individuals). Separation of biological samples and interspersed batches indicates that technical variation has been removed. We always use log2-cpm normalized data to match the assumptions of PCA.
for(n in assayNames(umi.qc)) {
tmp <- runPCA(umi.qc, exprs_values = n, ncomponents = 20)
print(
plotPCA(
tmp,
colour_by = "batch",
size_by = "detected",
shape_by = "individual"
) +
ggtitle(n)
)
}
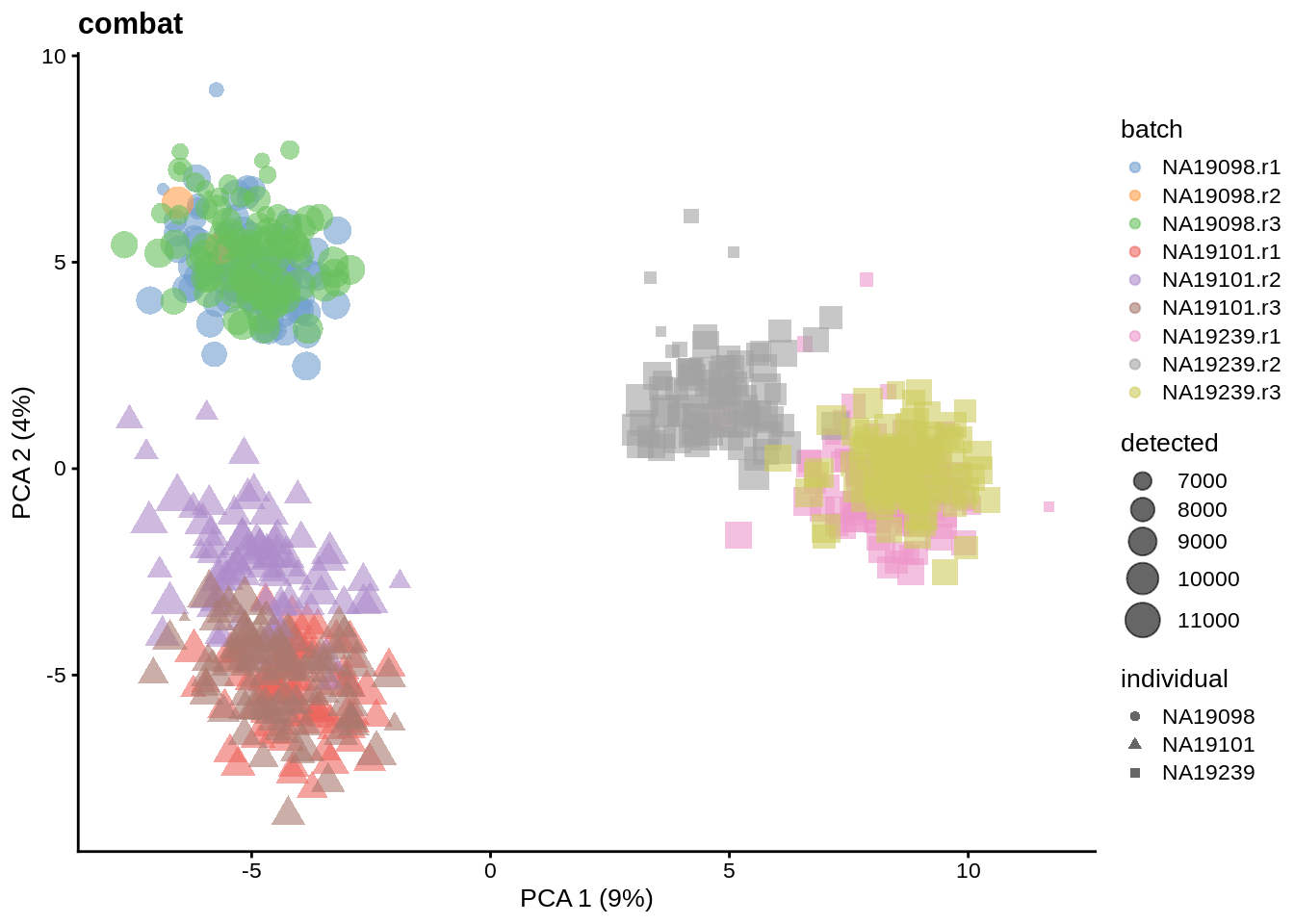
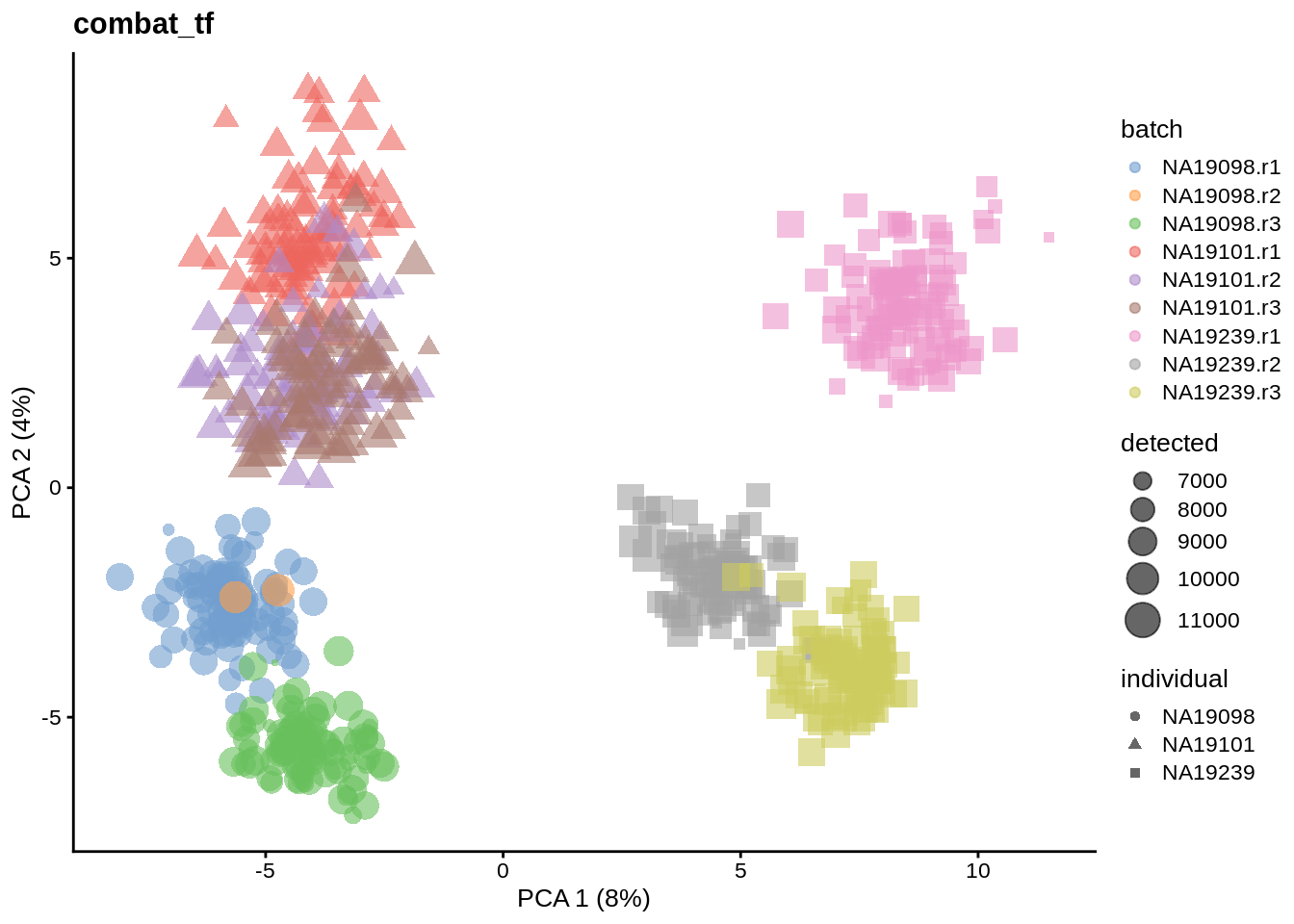
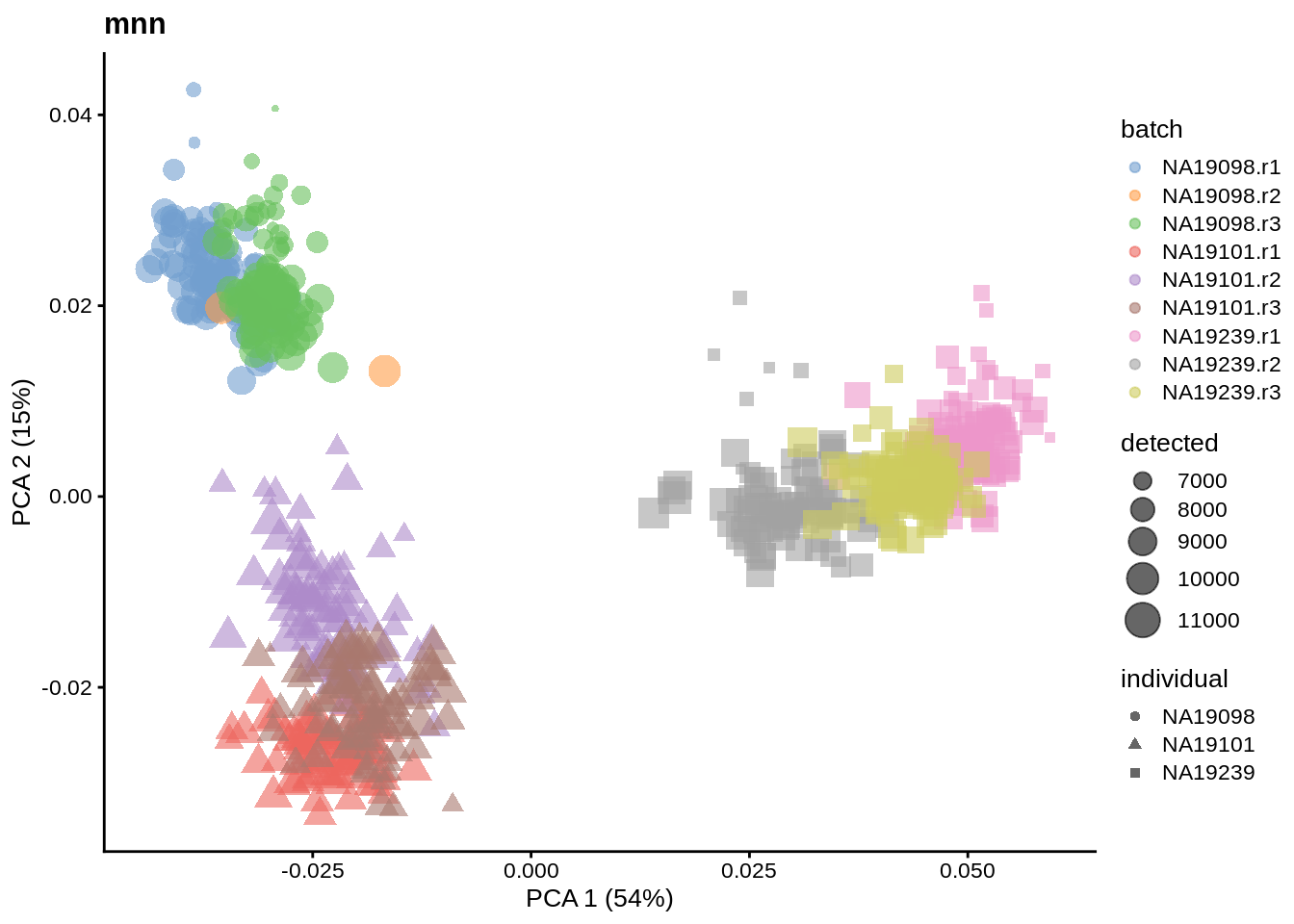
6.6.5.2 Effectiveness 2
We can also examine the effectiveness of correction using the relative log expression (RLE) across cells to confirm technical noise has been removed from the dataset. Note RLE only evaluates whether the number of genes higher and lower than average are equal for each cell - i.e. systemic technical effects. Random technical noise between batches may not be detected by RLE.
res <- list()
for(n in assayNames(umi.qc)) {
res[[n]] <- suppressWarnings(calc_cell_RLE(assay(umi.qc, n)))
}
par(mar=c(6,4,1,1))
boxplot(res, las=2)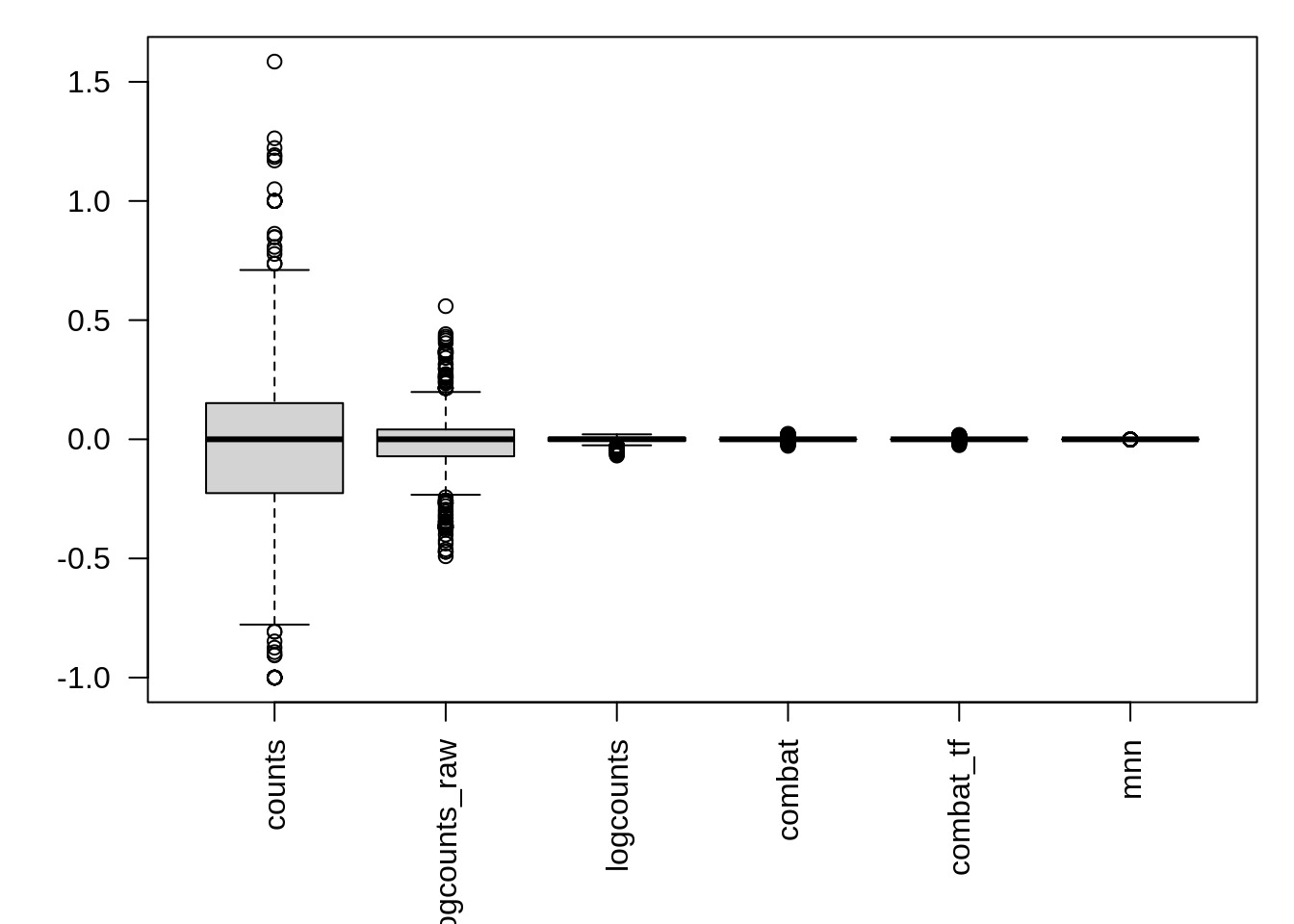
6.6.5.3 Effectiveness 3
Another method to check the efficacy of batch-effect correction is to consider the intermingling of points from different batches in local subsamples of the data. If there are no batch-effects then proportion of cells from each batch in any local region should be equal to the global proportion of cells in each batch.
kBET (Büttner et al. 2018) takes kNN networks around random cells and tests the number of cells from each batch against a binomial distribution. The rejection rate of these tests indicates the severity of batch-effects still present in the data (high rejection rate = strong batch effects). kBET assumes each batch contains the same complement of biological groups, thus it can only be applied to the entire dataset if a perfectly balanced design has been used. However, kBET can also be applied to replicate-data if it is applied to each biological group separately. In the case of the Tung data, we will apply kBET to each individual independently to check for residual batch effects. However, this method will not identify residual batch-effects which are confounded with biological conditions. In addition, kBET does not determine if biological signal has been preserved.
compare_kBET_results <- function(sce){
sce <- umi.qc
indiv <- unique(as.character(sce$individual))
norms <- assayNames(sce) # Get all normalizations
results <- list()
for (i in indiv){
for (j in norms){
tmp <- kBET(
df = t(assay(sce[,sce$individual== i], j)),
batch = sce$batch[sce$individual==i],
heuristic = TRUE,
verbose = FALSE,
addTest = FALSE,
plot = FALSE)
results[[i]][[j]] <- tmp$summary$kBET.observed[1]
}
}
return(do.call(rbind.data.frame, results))
}
eff_debatching <- compare_kBET_results(umi.qc)
eff_debatching## counts logcounts_raw logcounts combat combat_tf mnn
## NA19098 1.0000000 0.6220000 0.7264000 0.6228000 0.6632000 0.4596000
## NA19101 0.4268000 0.4492000 0.8120000 0.7832000 0.7488000 0.7312000
## NA19239 0.7055556 0.6851852 0.8918519 0.8688889 0.8240741 0.8814815Finally, let’s visualize the output of kBET calculation:
library("reshape2")
library("RColorBrewer")
# Plot results
dod <- melt(as.matrix(eff_debatching), value.name = "kBET")
colnames(dod)[1:2] <- c("Normalisation", "Individual")
colorset <- c('gray', brewer.pal(n = 9, "RdYlBu"))
ggplot(dod, aes(Normalisation, Individual, fill=kBET)) +
geom_tile() +
scale_fill_gradient2(
na.value = "gray",
low = colorset[2],
mid=colorset[6],
high = colorset[10],
midpoint = 0.5, limit = c(0,1)) +
scale_x_discrete(expand = c(0, 0)) +
scale_y_discrete(expand = c(0, 0)) +
theme(
axis.text.x = element_text(
angle = 45,
vjust = 1,
size = 12,
hjust = 1
)
) +
ggtitle("Effect of batch regression methods per individual")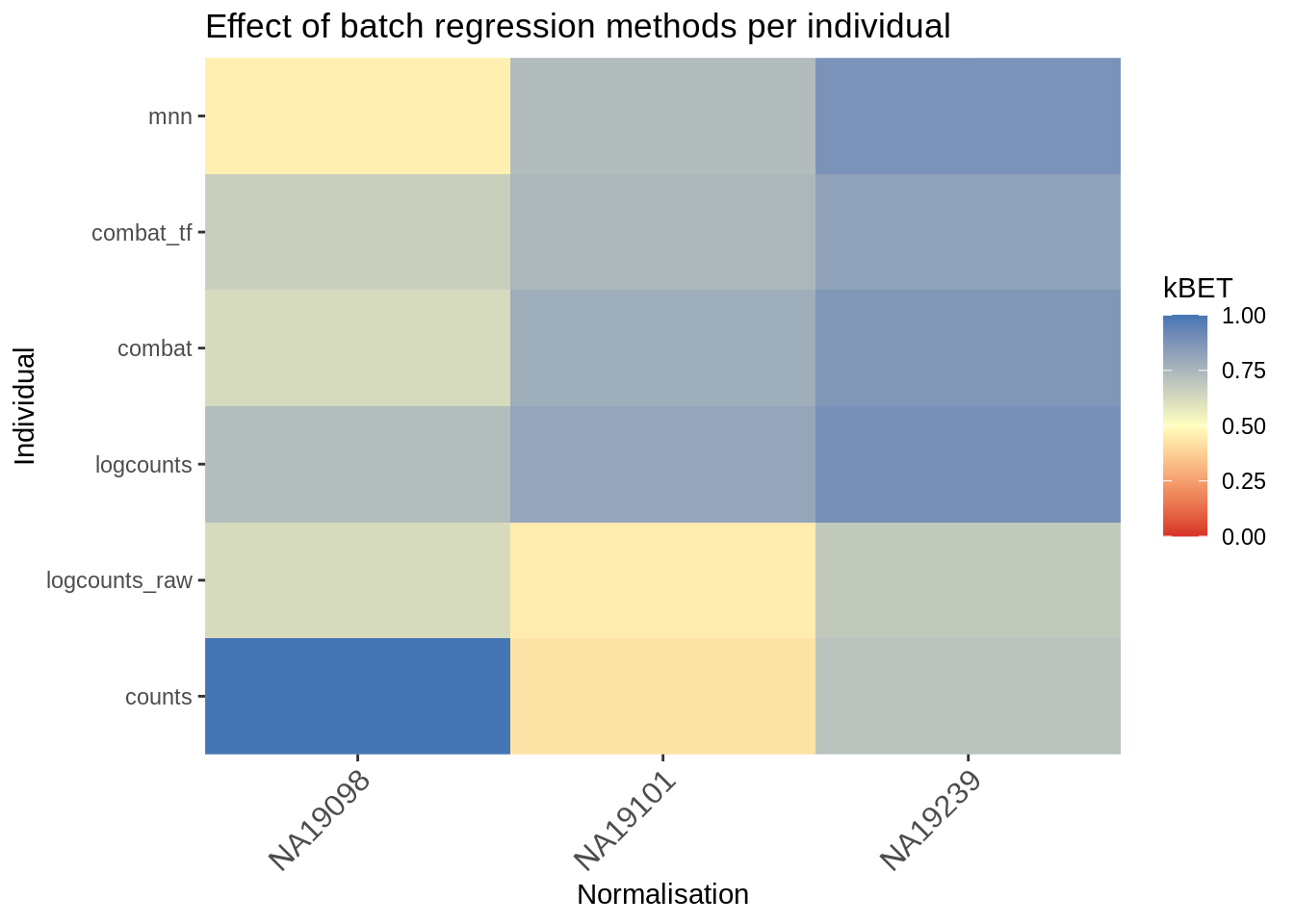
6.6.6 sessionInfo()
View session info
## R version 4.2.1 (2022-06-23)
## Platform: x86_64-pc-linux-gnu (64-bit)
## Running under: Ubuntu 20.04.2 LTS
##
## Matrix products: default
## BLAS: /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.9.0
## LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.9.0
##
## locale:
## [1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
## [3] LC_TIME=en_US.UTF-8 LC_COLLATE=en_US.UTF-8
## [5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
## [7] LC_PAPER=en_US.UTF-8 LC_NAME=C
## [9] LC_ADDRESS=C LC_TELEPHONE=C
## [11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
##
## attached base packages:
## [1] stats4 stats graphics grDevices utils datasets methods
## [8] base
##
## other attached packages:
## [1] RColorBrewer_1.1-3 reshape2_1.4.4
## [3] kBET_0.99.6 batchelor_1.12.3
## [5] sva_3.44.0 BiocParallel_1.30.3
## [7] genefilter_1.78.0 mgcv_1.8-40
## [9] nlme_3.1-157 scran_1.24.0
## [11] scater_1.24.0 ggplot2_3.3.6
## [13] scuttle_1.6.2 SingleCellExperiment_1.18.0
## [15] SummarizedExperiment_1.26.1 Biobase_2.56.0
## [17] GenomicRanges_1.48.0 GenomeInfoDb_1.32.2
## [19] IRanges_2.30.0 S4Vectors_0.34.0
## [21] BiocGenerics_0.42.0 MatrixGenerics_1.8.1
## [23] matrixStats_0.62.0 scRNA.seq.funcs_0.1.0
## [25] knitr_1.39
##
## loaded via a namespace (and not attached):
## [1] Rtsne_0.16 ggbeeswarm_0.6.0
## [3] colorspace_2.0-3 ellipsis_0.3.2
## [5] bluster_1.6.0 XVector_0.36.0
## [7] BiocNeighbors_1.14.0 farver_2.1.1
## [9] ggrepel_0.9.1 bit64_4.0.5
## [11] AnnotationDbi_1.58.0 fansi_1.0.3
## [13] codetools_0.2-18 splines_4.2.1
## [15] sparseMatrixStats_1.8.0 cachem_1.0.6
## [17] polynom_1.4-1 jsonlite_1.8.0
## [19] ResidualMatrix_1.6.0 annotate_1.74.0
## [21] cluster_2.1.3 png_0.1-7
## [23] compiler_4.2.1 httr_1.4.3
## [25] dqrng_0.3.0 assertthat_0.2.1
## [27] Matrix_1.4-1 fastmap_1.1.0
## [29] limma_3.52.2 cli_3.3.0
## [31] BiocSingular_1.12.0 htmltools_0.5.2
## [33] tools_4.2.1 rsvd_1.0.5
## [35] igraph_1.3.2 gtable_0.3.0
## [37] glue_1.6.2 GenomeInfoDbData_1.2.8
## [39] dplyr_1.0.9 Rcpp_1.0.9
## [41] jquerylib_0.1.4 Biostrings_2.64.0
## [43] vctrs_0.4.1 DelayedMatrixStats_1.18.0
## [45] xfun_0.31 stringr_1.4.0
## [47] beachmat_2.12.0 lifecycle_1.0.1
## [49] irlba_2.3.5 hypergeo_1.2-13
## [51] statmod_1.4.36 XML_3.99-0.10
## [53] edgeR_3.38.1 zlibbioc_1.42.0
## [55] MASS_7.3-58 scales_1.2.0
## [57] parallel_4.2.1 yaml_2.3.5
## [59] memoise_2.0.1 gridExtra_2.3
## [61] sass_0.4.1 stringi_1.7.8
## [63] RSQLite_2.2.14 highr_0.9
## [65] ScaledMatrix_1.4.0 orthopolynom_1.0-6
## [67] contfrac_1.1-12 rlang_1.0.4
## [69] pkgconfig_2.0.3 moments_0.14.1
## [71] bitops_1.0-7 evaluate_0.15
## [73] lattice_0.20-45 purrr_0.3.4
## [75] labeling_0.4.2 cowplot_1.1.1
## [77] bit_4.0.4 tidyselect_1.1.2
## [79] deSolve_1.32 plyr_1.8.7
## [81] magrittr_2.0.3 bookdown_0.27
## [83] R6_2.5.1 generics_0.1.3
## [85] metapod_1.4.0 DelayedArray_0.22.0
## [87] DBI_1.1.3 pillar_1.7.0
## [89] withr_2.5.0 survival_3.3-1
## [91] KEGGREST_1.36.3 RCurl_1.98-1.7
## [93] tibble_3.1.7 crayon_1.5.1
## [95] utf8_1.2.2 rmarkdown_2.14
## [97] viridis_0.6.2 locfit_1.5-9.6
## [99] grid_4.2.1 FNN_1.1.3.1
## [101] blob_1.2.3 digest_0.6.29
## [103] xtable_1.8-4 elliptic_1.4-0
## [105] munsell_0.5.0 beeswarm_0.4.0
## [107] viridisLite_0.4.0 vipor_0.4.5
## [109] bslib_0.3.1